Ребят Я в этом вообще не разбираюсь :(

1. Выразите в следующих уравнениях х через у и у через х:

1) а) х+у=5; б) x-y=0; в) y-x=-3;

2) a) x-3y=-6; б) -2x+y=3 в) x+5y=0

3) a) 2y-3x=0; б) 5x+2y=-10; в) -4x-7y=5,6.

2. Решите систему уравнений подстановки.

Выполните проверку, подставив полученное решение в

каждое из уравнений:

1) а) х+y=5, б) x-y=0, в) y-x=-3, г) -2x+y=3,

3х+y=7; x-3y=6; 2x+y=9; 3x-y=-1;

2) a) 3m-2n=5, б) a+3b=2, в) 3k-5p=14, г) 2c-d=2,

m+2n=15; 2a+3b=7; k+2p=1; 3c-2d=3;

Показать ответ

Ответ:

taniussa1

16.04.2023 07:24

По определению,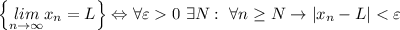 $\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение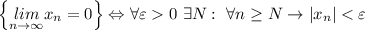 $\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

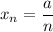
2) $x_n=\dfrac{a}{n}$

|x_n|

А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1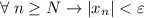$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: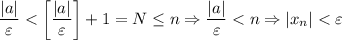 $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

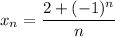
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1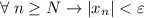$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда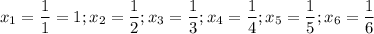 $x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$

___________________________

Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x.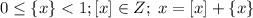 $0\leq \{x\}$

пример 2 и 4. Все теоремы и аксиомы, будьте добры, распишите. Действий, пусть и банальных, легких не

0,0(0 оценок)

Ответ:

Yuki16

08.01.2022 01:53

Интересная задачка.

Для того, чтобы начать решать эту задачу, нам необходимо найти такую последовательность, которая приносила бы нам всегда удачу! Из условия ясно, что начинающий должен ходить первый. Можно предложить такой вариант ходов:
Начинающий должен взять один карандаш. Остается 17 штук. Какое бы количество карандашей ни взял противник, обязательно нужно оставить 13 карандашей на столе. По такому же раскладу, надо оставить 9 карандашей, а затем 5. Какое бы количество карандашей не взял соперник, начинающий всегда сможет оставить ему 1 карандаш.

0,0(0 оценок)

Популярные вопросы: Алгебра