Делим уравнение на и обозначаем буквой q; . Получается уравнение
Угаданный корень x=5 для исходного уравнения приводит к корню q=1/7 полученного уравнения (подстановка подтверждает это). Докажем, что других корней нет. Для этого с производной убедимся, что левая часть убывает, а правая возрастает. С правой частью всё понятно, разберёмся с левой:
эта производная равна нулю при 4-3q=9(5+q); 12q=-41; q=-41/12∉(0;4/3]. Поэтому на интервале (0;4/3) производная не меняет знак. Легко убедиться, что этот знак отрицательный, устремив, например, q к 0. Поэтому функция f(q) убывает, а раз функция в правой части уравнения возрастает, другого решения кроме q=1/7 быть не может.
ответ: 5
Объяснение: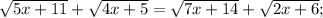 ОДЗ:
ОДЗ: 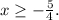
Корень x=5 угадываем (6+5=7+4 - верно). Замена: x+2=p; x=p-2;
эта производная равна нулю при 4-3q=9(5+q); 12q=-41; q=-41/12∉(0;4/3]. Поэтому на интервале (0;4/3) производная не меняет знак. Легко убедиться, что этот знак отрицательный, устремив, например, q к 0. Поэтому функция f(q) убывает, а раз функция в правой части уравнения возрастает, другого решения кроме q=1/7 быть не может.