Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
А
Английский язык
Х
Химия
Э
Экономика
П
Право
И
Информатика
У
Українська мова
Қ
Қазақ тiлi
О
ОБЖ
Н
Немецкий язык
Б
Беларуская мова
У
Українська література
М
Музыка
П
Психология
А
Алгебра
Л
Литература
Б
Биология
М
МХК
О
Окружающий мир
О
Обществознание
И
История
Г
Геометрия
Ф
Французский язык
Ф
Физика
Д
Другие предметы
Р
Русский язык
Г
География
Показать больше
Показать меньше
Vi0002
17.03.2022 18:45 •
Алгебра
Решить уравнение: 2cos^2x+sinx+1=0
Показать ответ
Ответ:
Vexicy
02.09.2020 07:18
.
Объяснение:
Пусть
Тогда уравнение принимает вид:
Условию
удовлетворяет t=-1.
0,0
(0 оценок)
Популярные вопросы: Алгебра
наст55
21.11.2021 04:14
Часть 1. а1. выражение -4m + 9n - 7m - 2n. 1)-3m + 11n 2) -3m + 7n 3) 11m + 7n 4) -11m + 7n a2. решите уравнение 5у + 1,5 = 2у - 7,5. 1)6,375 2)3 3)-3 4)4 a3. выражение...
Goodmegaparadise
09.07.2021 14:27
1/2*(cos(5x-x)+cos(5x+=0 1/2*cos4x+1/2*cos6x-cos4x=0 а как дальше? разъясните...
musalimovvlad
09.07.2021 14:27
Подобные слагаемые в сумме: а)-6x+5x-6x б) 3m-10m-11n-m+12n...
adilyaarslanov
23.09.2021 16:29
1) x степень 2 , -x степень 2 (-x) степень 2 , если x=5; -4; 2) x степень 3 , -x степень 3 (-x)степень 3 , если x=3; -2....
marichkakyhar
01.08.2020 16:59
1: четное или не четное y=cosx-x^2 2 : найдите наибольшее и наименьшее значения функции у = 3 sin x cos x + 1 ответы дайте с решениями заранее...
evegn1331
01.08.2020 16:59
Найти площадь четырехугольника авсд, если ав=вс=12 см, сд=18 см, вд=6 корень из 5, да = 6 см...
миккимаус1890677
01.08.2020 16:59
Вгруппе туристов 20 человек. их забрасывают в труднодоступный район вертолетом в несколько приемов по 5 человек за рейс. порядок, в котором вертолет перевозит туристов,...
vadimmoroz903
10.01.2020 05:59
Выразить k из равенства 9 делить на 2 равно p-k делить на 18...
danul1414
25.01.2020 19:38
Вычислите дискриминант уравнения и ответьте на следующие вопросы: 1)имеет ли уравнение корни; 2)если имеет,то сколько; 3)рациональными или иррациональными числами являются...
danilrykov200
25.01.2020 19:38
Найдите сумму корней уравнения 2х^2-5х+1=0 теорема виета там надо выбрать ответ а)12целых семь восьмых б)12целых восемь девятых в)11целых семь восьмых г)12 целых...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Объяснение:
Пусть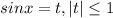 Тогда уравнение принимает вид:
Тогда уравнение принимает вид:
Условию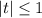 удовлетворяет t=-1.
удовлетворяет t=-1.