1 шаг. Проверим справедливость утверждения при n=1:
- верно
2 шаг. Предположим, что при n=k следующее утверждение верно:
3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:
Для доказательства выполним преобразования:
Рассмотрим получавшуюся сумму. Первое слагаемое делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
Мы получили, что выражение дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение кратно 3.
Возвращаясь к выражению , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
First, we'll try to plug in the value: #lim_{x to -oo}x+sqrt(x^2+2x) = -oo + sqrt(oo-oo)# We're already encountering a problem: it is simply not allowed to have #oo-oo#, it's like dividing by zero. We need to try a different approach. Whenever I see this kind of limit, I try to use a trick: #lim_{x to -oo}x+sqrt(x^2+2x)# #= lim_{x to -oo}x+sqrt(x^2+2x)*(x-sqrt(x^2+2x))/(x-sqrt(x^2+2x))# These are the same becaus the factor we're multiplying with is essentially #1#. Why are we doing this? Because there exists a formula which says: #(a-b)(a+b) = a^2-b^2# In this case #a = x# and #b = sqrt(x^2+2x)# Let's apply this formula: #lim_{x to -oo}(x^2-(sqrt(x^2+2x))^2)/(x-sqrt(x^2+2x))# #= lim_{x to -oo}(x^2-x^2-2x)/(x-sqrt(x^2+2x))# #= lim_{x to -oo}(-2x)/(x-sqrt(x^2+2x))# Now we're going to use another trick. We'r going to use this one, because we want to get the #x^2# out of the square root: #lim_{x to -oo}(-2x)/(x-sqrt(x^2(1+2/x))# If you look carefully, you see it's the same thing. Now, you might say that #sqrt(x^2) = x#, but you have to remember that #x# is a negative number. Because we're taking the positive square root, #sqrt(x^2) = -x# in this case. #= lim_{x to -oo}(-2x)/(x+xsqrt(1+2/x))# #= lim_{x to -oo}(-2x)/(x(1+sqrt(1+2/x)))# We can cancel the #x#: #= lim_{x to -oo}(-2)/(1+sqrt(1+2/x))# And now, we can finally plug in the value: #= -2/(1+sqrt(1+2/-oo))# A number divided by infinity, is always #0#: #= -2/(1+sqrt(1+0)) = -2/(1+1) = -2/2 = -1# This is the final answer. Hope it helps.
1 шаг. Проверим справедливость утверждения при n=1:
2 шаг. Предположим, что при n=k следующее утверждение верно:
3 шаг. Докажем, что при n=k+1 следующее утверждение также будет верно:
Для доказательства выполним преобразования:
Рассмотрим получавшуюся сумму. Первое слагаемое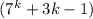 делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом
делится на 9 по предположению, сделанному на предыдущем шаге. Во втором слагаемом 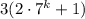 первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
первый множитель делится на 3. Значит, остается доказать, что второй множитель также делится на 3. Докажем это, используя арифметику остатков:
Мы получили, что выражение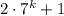 дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение
дает при делении на 3 такой остаток, как и число 3. Но число 3 кратно 3, значит и выражение 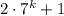 кратно 3.
кратно 3.
Возвращаясь к выражению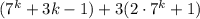 , повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
, повторим, что первое слагаемое делится на 9, второе слагаемое представляет собой произведение двух множителей, каждое из которых делится на 3, то есть само слагаемое делится на 9. Сумма двух выражений, делящихся на 9, также делится на 9, или другими словами, кратна 9. Доказано.
#lim_{x to -oo}x+sqrt(x^2+2x) = -oo + sqrt(oo-oo)#
We're already encountering a problem: it is simply not allowed to have #oo-oo#, it's like dividing by zero.
We need to try a different approach.
Whenever I see this kind of limit, I try to use a trick:
#lim_{x to -oo}x+sqrt(x^2+2x)#
#= lim_{x to -oo}x+sqrt(x^2+2x)*(x-sqrt(x^2+2x))/(x-sqrt(x^2+2x))#
These are the same becaus the factor we're multiplying with is essentially #1#.
Why are we doing this? Because there exists a formula which says: #(a-b)(a+b) = a^2-b^2#
In this case #a = x# and #b = sqrt(x^2+2x)#
Let's apply this formula:
#lim_{x to -oo}(x^2-(sqrt(x^2+2x))^2)/(x-sqrt(x^2+2x))#
#= lim_{x to -oo}(x^2-x^2-2x)/(x-sqrt(x^2+2x))#
#= lim_{x to -oo}(-2x)/(x-sqrt(x^2+2x))#
Now we're going to use another trick. We'r going to use this one, because we want to get the #x^2# out of the square root:
#lim_{x to -oo}(-2x)/(x-sqrt(x^2(1+2/x))#
If you look carefully, you see it's the same thing.
Now, you might say that #sqrt(x^2) = x#, but you have to remember that #x# is a negative number. Because we're taking the positive square root, #sqrt(x^2) = -x# in this case.
#= lim_{x to -oo}(-2x)/(x+xsqrt(1+2/x))#
#= lim_{x to -oo}(-2x)/(x(1+sqrt(1+2/x)))#
We can cancel the #x#:
#= lim_{x to -oo}(-2)/(1+sqrt(1+2/x))#
And now, we can finally plug in the value:
#= -2/(1+sqrt(1+2/-oo))#
A number divided by infinity, is always #0#:
#= -2/(1+sqrt(1+0)) = -2/(1+1) = -2/2 = -1#
This is the final answer.
Hope it helps.