Чтобы изобразить график линейной функции вида где и — коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение подставляйте его в функцию и находите (Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции
Строим таблицу для двух точек:
Пусть
Тогда
Пусть
Тогда
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точки: и — и проведем через них прямую (см. вложение). График линейной функции построен.
a)y(наиб)=2
y(наим)=-2
b)y(наим)=-29
y(наиб)=31
Объяснение:
a)
1)Находим производную функции :
f'(x)=3x^2-3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2-3=0 --> x=1
x=-1
3) Промежутку принадлежит только точка x=1 , поэтому значения функции на концах и в точке 1:
f(0)=0
f(1)=-2-наим
f(2)=8-6=2-наиб
б)
1)Находим производную функции :
f'(x)=3x^2+3
2) Приравниваем производную к 0 ( находим нули производной):
3x^2+3=0 --> решений нет , значит наибольшее значение достигает правом конце отрезка [-3;3] , а наименьшее - в левом:
3) f(-3)=-27-3+1=-29
f(3)=27+3+1=31
Чтобы изобразить график линейной функции вида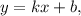
где 
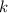и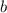 
— коэффициенты, достаточно на координатной плоскости отметить две точки и провести через них прямую.
Для этого строят таблицу для двух точек: первая строка — абсцисса (иксы), вторая строка — ордината (игреки). Вы — хозяин своей таблицы. Подбирайте любое значение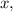
подставляйте его в функцию и находите 
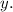(Подбирайте числа в пределах разумного.)
Пример. Изобразить график линейной функции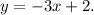
Строим таблицу для двух точек:
Пусть
Тогда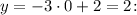
Пусть
Тогда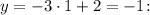
Имеем заполненную таблицу для двух точек. Изобразим координатную плоскость, отметим две точк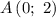и:
и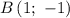 
— и проведем через них прямую (см. вложение). График линейной функции 
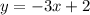построен.