Войти Регистрация Спроси ai-bota

Решите уравнение квадратноая скобка(3x-54)8-159 квадратная скобка:21=21

Показать ответ

Ответ:

костя663

13.09.2022 14:57

Х - скорость лодки в неподвижной воде
Плот проплыл 36 км за 36 / 4 = 9 часов . По условию задачи имеем : 126/(х + 4) + 126/ (х - 4) = 9 - 1
126 *(х - 4) + 126 * (х + 4) = 8 * (x^2 - 16)
126x - 504 + 126x + 504 = 8x^2 - 128
8x^2 - 252x - 128 = 0
2x^2 - 63x - 32 = 0 . Найдем дискриминант D квадратного уравнения и найдем корни этого уравнения . D = 63^2 - 4 * 2 * (- 32) = 3969 + 252 = 4225 . Корень квадратный из дискриминанта : 1- ый = (-(-63 + 65)) /2 * 2= 128 / 4 = 32 .; 2 - ой = (-(-63) - 65)/ 2*2 = - 2 / 4 = - 0,5 . Второй корень не подходит , так как скорость не может быть меньше 0 .
Сбственная скорость равна : 32 км/час

0,0(0 оценок)

Ответ:

lisovasvitlana15

01.07.2022 21:09

Задание № 1.

а).

Просто подставляем в уравнение, задающее функцию,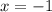 x=-1 :

$f(-1) = 2 \cdot (-1)^2-5 \cdot (-1) +3 = 2 + 5 + 3 = 10$

б).

Найдем те значения , при которых значение функции становится равным :

$\displaystyle 1 = 2x^2-5x+3\\\\2x^2 - 5x + 2 = 0\\\\x_1 = \frac{- b + \sqrt{b^2-4ac} }{2a} = \frac{5 + \sqrt{9} }{4} = 2 \\\\x_1 = \frac{- b - \sqrt{b^2-4ac} }{2a} = \frac{5 - \sqrt{9} }{4} = 0,5$

в).

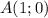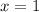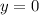Для того, чтобы определить, принадлежит ли точка A(1;0) графику, подставим в уравнение функции x=1 и y=0 , и посмотрим, что получится:

$y=2x^2-5x+3\\\\0 = 2 \cdot 1^2 - 5 \cdot 1 + 3\\\\0 = 0$

Получилось верное равенство! Значит, точка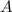 действительно принадлежит графику рассматриваемой функции.

___________________________________________

Задание № 2.

а).

Задача заключается в решении неравенства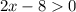 2x-80 :

$f(x) = 2x - 8 0 \\\\2x-8 0\\\\2x 8 \\\\x 4$

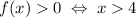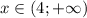Получаем, что $f(x) 0 \; \Leftrightarrow \; x4$ , или $x \in (4; + \infty)$ .

б).

Ноли функции - это те значения , при которых f(x)=0 :

$f(x) = 2x - 8 = 0\\\\2x=8 \\\\x=4$

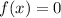Значит, единственный ноль функции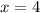 x=4 .

___________________________________________

Задание № 3.

а).

Область определения функции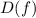 D(f) - это те значения , при которых функция существует.

А функция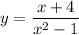 $y= \dfrac{x+4}{x^2 - 1}$ существует только в том случае, если ее знаменатель не равен нолю:

$\displaystyle x^2 - 1 \neq 0 \; \Leftrightarrow \; \left \{ {{x \neq -1 } \atop {x \neq 1}} \right.$

То есть, область определения данной функции - все действительные , кроме $x = \pm 1$ :

$x \in ( - \infty ; -1 ) \cup (-1 ; 1) \cup (1 ; + \infty )$

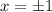Задача решена!

Функция задана формулой f(x)=2x^2-5x+3 a)найдите f(-1) б)определите, при каких значениях x выполняет

0,0(0 оценок)

Популярные вопросы: Алгебра

двоишник54

31.08.2021 04:23

Задание дам 20 минут и...

lenya013

13.05.2020 18:06

В спортивной школе есть секция шахмат и секция настольного тенниса. Каждый ученик спортивной школы ходит либо на секцию шахмат, либо на секцию настольного тенниса. Каждый шахматист...

Sofia1986

16.07.2022 15:20

6. Жәшікте 3 ақ және 12 қызыл шар бар. Жәшіктен бір шар алынды. Алынған шардың қызыл түсті болуының ықтималдығын табыңдар: A. 0,7 B. 0,2 C. 0,8 D. 0,75 E. 0,4...

милана200229

09.08.2020 05:26

1.Выяснить, при каких значениях х имеет смысл выражение: 1) log22(4-x) 2) log0,3(x2 -8x+7) 3) log0,2(7-x) 4) log8(x2 -8x+15)...

koi4

30.11.2020 09:29

Втреугольнике авс угол с=90°,sin b=15/17,ac=30., найти ав...

Mafg

30.11.2020 09:29

Hlp 1)дана функция g(x)=log1/3x вычислить значение аргумента, если значение функции равно -3 2)укажи область определения функции y=log0,6(x^2−14x+40) корни квадратного уравнения...

Motcic

30.11.2020 09:29

Скажите 9пи/2 какая формула там используется?...

cmh3

30.11.2020 09:29

Добрый вечер, господа! соизвольте снизойти с небес и по , ) 1. выражение (a3-9a/a2+6a+9)-a и найдите его значение при a= -(1/2) 2.арифметическая прогрессия задана условием...

Kyki510

30.11.2020 09:29

Представьте квадрат двучлена в виде многочлена: (5-6d^5)^2...

Lalikolalik

03.05.2021 11:09

Найдите произведение корней уравнения lg^2 x-3lg x-10=0...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку