a) Так как отрезки AB и BC являются диагоналями одинаковых прямоугольников со сторонами 2х4 ⇒ AB = BC. А если в треугольнике две стороны равны ⇒ треугольник является РАВНОБЕДРЕННЫМ.
b) Координаты точки K по рисунку = (6; 5).
с) Так как BK является медианой равнобедренного Δ ABC ⇒ она совпадает с его ВЫСОТОЙ. А так же её длинна = половине отрезка AC
Площадь треугольника вычисляется по формуле:
a - основание треугольника (в нашем случае AC);
h - высота треугольника (в нашем случае BK).
Для того чтобы узнать длину основания треугольника AC - построим ещё один прямоугольный треугольник Δ ACZ, у которого AZ и ZC - катеты, а AC - гипотенуза.
По теореме Пифагора:
На рисунке длина AZ = 6 ед.; длина ZC = 2 ед.
Подставляем эти значения в формулу, и вычисляем длину AC:
⇒
Зная длину основания и высоты треугольника - вычисляем его площадь:
b) Координаты точки K по рисунку = (6; 5).
с) Так как BK является медианой равнобедренного Δ ABC ⇒ она совпадает с его ВЫСОТОЙ. А так же её длинна = половине отрезка AC
Площадь треугольника вычисляется по формуле:
a - основание треугольника (в нашем случае AC);
h - высота треугольника (в нашем случае BK).
Для того чтобы узнать длину основания треугольника AC - построим ещё один прямоугольный треугольник Δ ACZ, у которого AZ и ZC - катеты, а AC - гипотенуза.
По теореме Пифагора:
На рисунке длина AZ = 6 ед.; длина ZC = 2 ед.
Подставляем эти значения в формулу, и вычисляем длину AC:
⇒
Зная длину основания и высоты треугольника - вычисляем его площадь:
Объяснение:
y = -x
1) Функция имеет единственный ноль к точке (0, 0)
2) Область определения функции ( -∞ ; +∞)
3) Область значений такая же, т.е. ( -∞ ; +∞)
4) Область определения совпадает с областью значений
5) Функция располагается в 2 и 4 четвертях
6) Функция положительна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент отрицателен
7) Функция отрицательна ТОГДА И ТОЛЬКО ТОГДА, когда её аргумент положителен
8) Это монотонно убывающая функция
9) Функция убывает на всей своей области определения
10) Функция не имеет периода
11) График этой функции - прямая, проходящая через центр координат
12) Это нечётная функция
13) Тангенс угла наклона касательной к точке графика постоянен и равен -1 для всех х
14) Площадь под графиком от 0 до х равна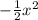
Здесь все свойства функции, выбирайте нужные.
На графике красным - сам график
Голубым подписаны четверти, их подписывать не обязательно.