Решите уравнение с объяснением
s(n)-сумма цифр числа

n=s(n)+218

Показать ответ

Ответ:

murplushka

08.03.2023 04:32

Объяснение:

Формула разности квадратов а²-в²=(а-в)(а+в) ;

(а-в)²=(в-а)²

6) ( 2х-о,5у)²-(х-у)²= ( ( 2х-о,5у)- (х-у) ) ( ( 2х-о,5у) + (х-у) )=

= ( 2х-о,5у- х+у ) ( 2х-о,5у + х-у )=(х-0,5у)(3х-1,5у)=

=1,5(х-0,5у)(2х-у)

7) (5а-2)³+(2-5а)²= (5а-2)³+1*(5а-2)²= вынесем общий множитель за скобку=(5а-2)²(5а-2+1)=(5а-2)²(5а-1).

8)( 0,2а-в)²-(а-0,2в)²= формула разности квадратов=

=( ( 0,2а-в)-(а-0,2в) )( ( 0,2а-в)+(а-0,2в) )=

=( 0,2а-в-а+0,2в )( 0,2а-в+а-0,2в )=(-0,8а-0,8в)(1,2а-1,2в)=

=-0,8*1,2(а+в)(а-в)=-0,96(а+в)(а-в).

9) аналогично 7 ( см в комментариях)

10) 1,21х²-0,36у⁶=(1,1х)²-(0,6у³)²= разность квадратов=

=(1,1х-0,6у³)( 1,1х+0,6у³).

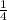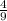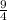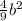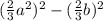11)2 $\frac{1}{4}$ *а⁴ - $\frac{4}{9}$ *в²= $\frac{9}4}$ а⁴ - $\frac{4}{9} b^{2}$ = $(\frac{2}3} a^{2} )^{2} -(\frac{2}{3} b)^{2}$ =

=(1,5a²-2/3в²) (1,5a²+2/3в²).

12) 1,69х⁸y⁸-9=(1,3х⁴у⁴)²-3²= (1,3х⁴у⁴-3) (1,3х⁴у⁴+3)

0,0(0 оценок)

Ответ:

Ksuha1304

04.03.2023 00:00

Объяснение:

Заметим, что сумма цифр у числа будет иметь такой же остаток по модулю 9, что и само число, так как пусть число имеет вид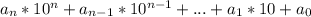 $a_{n}*10^n + a_{n-1}*10^{n-1} + ... +a_1*10+a_0$ заметим, что число вида 10^n-1 делится на 9, так как оно будет состоять из одних девяток, значит число вида 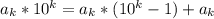a_k*10^k = a_k*(10^k-1) + a_k сравнимо с 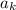a_k по модулю 9. Значит все число сравнимо с суммой цифрой по модулю 9. Так как 209! делится на 9 (содержит множитель 9), то сумма цифр будет делится на 9 ⇒ сумма суммы цифр делится на 9 и. т.д. Таким образом, однозначное число будет делится на 9, значит оно равно 0 или 9, но равно 0 оно быть не может, так как сумма цифр у натурального числа ненулевая, так как содержит хотя бы 1 не 0. Значит она равна 9