1) по теореме косинусов имеем: a² = b² + c² - 2bc cos a = 25 - 24 cos 135° = 25 + 12√2 a = √(25 + 12√2) по теореме синусов, a / sin a = b / sin b sin b = sin a · b / a = √2 / 2 · 3 / √(25 + 12√2) = 3 / √(50 + 24√2) ∠b = arcsin(3 / √(50 + 24√2)) ∠c = 180° - 135° - ∠b = 45° - arcsin(3 / √(50 + 24√2)) 2) ∠a = 180° - ∠b - ∠c = 65° по теореме синусов b / sin b = a / sin a b = a sin b / sin a = 24.6 · √2 / 2 / (sin 65°) = 123√2 / (10 sin 65°) по теореме синусов c / sin c = a / sin a c = a sin c / sin a = 24.6 ·sin 70° / sin 65°
3)x=
4)x=
Объяснение:
3)
Умножаем обе части():
3(6x-1)-4(3x+1)=3
Распределить 3 и 4 через скобки:
18x-3-4(3x+1)=3
18x-3- 12x - 4=3
Привести подобные члены:
6x-3-4=3
6x-7=3
Переносим постоянную(-7) в правую часть и сменяем ее знак:
6x=3+7
Вычисляем:
6x=10
Разделим обе стороны на 6:
x=
4)
Раскрываем скобки:
Умножаем обе части уравнения на 4:
2(2x-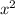
)+3x+2
Распределяем 2 через скобки(2(2x-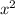
)):
4x-2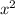
+3x+2
Поскольку сумма двух противоположных величин равна нулю, надо удалить их из выражения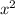(-2
и 2
4x+3x=4
7x=4
Разделить обе стороны на 7:
x=
Надеюсь
:)