2 корня
Объяснение:
x⁴+ax²+b=0
Данное уравнение является биквадратным и должно иметь 4 корня. По условию, оно имеет три корня, т.е. три действительных корня. При b=0 это возможно.
Покажем это:
Замена: x²=y
y²+ay+b=0
При b=0 y²+ay=0
y(y+a)=0
y=0 или y+a=0
y=-a
Обратная замена: y=x²
x²=0 или x²= -a
x₁=0 x₂=√-a x₃=-√-a
Итак, уравнение x⁴+ax²+b=0 имеет три корня
При b=0 уравнение x⁴+bx²+a=0 при b=0 преобразуется в уравнение
x⁴+a=0
x⁴= -a
Получаем, что это уравнение имеет два корня
Легко заметить, что оба уравнения имеют корни x=±1
Уравнение
имеет корни: x=±1
значит
⇒
Уравнение принимает вид:
Третий корень только
при
Тогда
при и
принимает вид:
и имеет два корня x=±1
2 корня
Объяснение:
x⁴+ax²+b=0
Данное уравнение является биквадратным и должно иметь 4 корня. По условию, оно имеет три корня, т.е. три действительных корня. При b=0 это возможно.
Покажем это:
Замена: x²=y
y²+ay+b=0
При b=0 y²+ay=0
y(y+a)=0
y=0 или y+a=0
y=-a
Обратная замена: y=x²
x²=0 или x²= -a
x₁=0 x₂=√-a x₃=-√-a
Итак, уравнение x⁴+ax²+b=0 имеет три корня
При b=0 уравнение x⁴+bx²+a=0 при b=0 преобразуется в уравнение
x⁴+a=0
x⁴= -a
Получаем, что это уравнение имеет два корня
Легко заметить, что оба уравнения имеют корни x=±1
Уравнение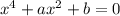
имеет корни: x=±1
значит
Уравнение принимает вид:
Третий корень только
при
Тогда
Уравнение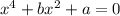
при и
и 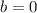
принимает вид:
и имеет два корня x=±1