с решением Заранее Датчик измеряет уровень воды в водохранилище по отношению к ординару ( нормальному уровню). Расположите события в порядке возрастания их вероятностей:
1) уровень воды не ниже ординатора
2) уровень между отметками 1,2 и 1,9 м выше ординара
3) уровень выше отметки "0,9 м выше ординара"
4) уровень выше отметки "0,5 м выше ординара"
В ответе запишите последовательность цифр без пробелов и других посторонних знаков.
0,4
Объяснение:
Пронумерую места на скамейке от 1 до 5, нумерация слева направо. Общее число вариантов рассадки относительно этих мест = 5! = 5*4*3*2*1 = 120 (на первое место могут сесть 5 человек, на второе - 4, т.к. кто-то уже сидит, и т.д.).
Пусть первая девочка сидит левее второй. Тогда если они сидят вместе, то на местах соответственно: 1 и 2, 2 и 3, 3 и 4, 4 и 5 - 4 варианта. Для каждого варианта есть 3! = 6 вариантов рассадки мальчиков (девочки зафиксированы на своих местах). Тогда суммарно в этом случае будет 4*6 = 24 подходящих случая. Если они поменяются местами - это ещё 24 варианта, итого 48 нужных вариантов из 120, т.е. вероятность равна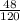
= 0,4.
Число a должна иметь вид : a =36k +18 .
Т.к. число a трехзначное, то 100<36k+18 <1000 ⇔3 ≤ k ≤ 27.
Количество таких чисел: n=27-(3-1) = 25 .
a∈{ 126 ; 162 , 198 ; ...972} * * * Составляют арифметическую прогрессию * * *
* ! 702 = 126 +(n-1)36⇒n=17 * * *
702 =36k+18 при k =19.
* * * P.S. * * *
a = 9x = 4y +2 ; || 100 <9x <1000⇔12 <x ≤111 ||
y =(9x -2)/4 ;
y = 2x + (x-2)/4 ; k= (x-2)/4⇒x=4k+2 . || y =2x+k =2(4k+2)+k =9k+4 ||
⇒ { x =4k +2 . y =9k+4 .
|| 12 ≤ 4k+2 ≤ 111⇔2,5 ≤ k ≤27,25 ; 3 ≤ k ≤ 27 ||
a =9x =36k+18.
число a =9x =9(4k +2) =36k +18.