с заданием! Вычислить несобственные интегралы или установить их расходимость:

Объяснение:

Подыинтегральная функция на указанном промежутке интегрирования имеет единственную особенность в точке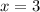 . Исследовать интеграл на сходимость в этой точке можно с признака сравнения. В окрестности данной точки данный интеграл эквивалентен интегралу:

то есть исходный интеграл сходится на заданном промежутке. Найдем его: