Сделать в виде реферата I часть :
Построение графика членов арифметической прогрессии.
2) Пусть задана арифметическая прогрессия (любая), например, (аn) = 3n+1
3) Найти область определения (множество значений), область допустимых значений
4) Пометка : Каждому натуральному числу ставится в соответствии какое-то одно число (а1, а2, а3 и т.д.)
Например, а1 - 1, а2 - 2, а3 - 3
5) Лучше взять n до 5 члена арифметической прогрессии
6) Построить таблицу для графика функции
7) Построить график в прямоугольной системе координат, он будет состоять из точек, но нужно будет соединить их, чтобы показать как они расположены
8) График подписать
II часть :
1) Построение графика членов геометрической прогрессии
2) Пусть дана геометрическая прогрессия, например, (bn), b1 = 3, q = ½
3) Найти область определения, область допустимых значений
4) смотри выше, как с арифметической прогрессией в 4)
5) Написать где-нибудь после графика :
"Зависимость bn от n для членов геометрической прогрессии получила название экспоненциональной
6) Сделать таблицу для графика функции
7) Нарисовать график на прямоугольной системе координат, все точки соединить плавной линией, должна получится кривая
8) график подписать
Рабочие производили детали 17 дней и произвели 1156 деталей.
Объяснение:
Допустим x - максимальное количество дней. Тогда x-2 - это количество затраченных дней.
(x-2)*68 = 60x - если производить 68 деталей в день x-2 дней, то получится то же кол-во, если производить 60 деталей x дней.
Решаем уравнение
68x-136 = 60x
68x - 60x = 136
8x = 136
x = 136/8
x = 17
ответ: на изготовление деталей ушло 17 дней.
Рабочие 17 дней производили 68 деталей в день. Значит кол-во деталей равно 17*68
17*68 = 1156
ответ: 1156 деталей произвели рабочие.
Если есть вопросы, пиши
25
Объяснение:
решения.
Выпишем несколько первых натуральных чисел кратных 5:
5, 10, 15, 20, 25, 30, 35, 40, 54, ... (далее каждое пятое натуральное число будет являться членом данной последовательности).
Пронумеруем члены последовательности:
Число, следующее за четвертым членом последовательности 25.
решения.
Воспользуемся формулой для нахождения n-го члена арифметической последовательности.
Наименьшее натуральное число делящееся на 5 это 5, т.е.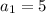 .
.
Далее каждое пятое натуральное число делится на 5. Значит разность арифметической прогрессии равна 5, т.е.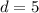 .
.
Т.к. по условию нужно найти число, следующее за a₄, то находим а₅.