V=(40-X)(64-X)X - функция. найти максимум, х∈(0, 40). найдем производную от V=(40-X)(64-X)X=х³-104х²+2560х она равна 3х²-208х+2560 найдем стационарные точки , приравняв производную к 0 , и решив кв. ур-ние 3х²-208х+2560=0 1) х=(104+√(104²-3·64·40))/3=(104+√((8·13)²-3·64·40)))/3= =(104+√(8²(13²-3·40)))/3=(104+8√(13²-3·40))/3=(104+8√(169-120))/3= =(104+8·7)/3=160/3
2) х=(104-√(104²-3·64·40))/3=(104-56)/3=16 ОСТАЛОСЬ по достаточному условию экстремума убедиться, что х=16 - точка максимума, проверяем знаки производной при переходе через эту точку, решаем неравенство 3х²-208х+2560>0, или простыми вычислениями для значений х из соответствующих промежутков.)
Поэтому, если задано уравнение, где в левой части стоит произведение каких-то выражений, а в правой части записан 0, то его очень легко решать, так как произведение равно нулю, когда какой-либо из множителей равен 0.
(х-4)(х-5)(х-6)=0 , если либо (х-4)=0, либо (х-5)=0 , либо (х-6)=0 .
То есть либо х=4 , либо х=5 , либо х=6 .
Значит мы получили три значения переменной "х", при которых левая часть обратиться в 0 . Это и есть корни уравнения.
Проверим, подставим вместо "х" значение 4, получим
найти максимум, х∈(0, 40).
найдем производную от V=(40-X)(64-X)X=х³-104х²+2560х
она равна 3х²-208х+2560
найдем стационарные точки , приравняв производную к 0 , и решив кв. ур-ние 3х²-208х+2560=0
1) х=(104+√(104²-3·64·40))/3=(104+√((8·13)²-3·64·40)))/3=
=(104+√(8²(13²-3·40)))/3=(104+8√(13²-3·40))/3=(104+8√(169-120))/3=
=(104+8·7)/3=160/3
2) х=(104-√(104²-3·64·40))/3=(104-56)/3=16
ОСТАЛОСЬ по достаточному условию экстремума убедиться, что х=16 - точка максимума, проверяем знаки производной при переходе через эту точку, решаем неравенство 3х²-208х+2560>0, или простыми вычислениями для значений х из соответствующих промежутков.)
вот как-то так...-))
При умножении любого числа на 0 мы получаем 0 !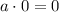 !
!
Поэтому, если задано уравнение, где в левой части стоит произведение каких-то выражений, а в правой части записан 0, то его очень легко решать, так как произведение равно нулю, когда какой-либо из множителей равен 0.
(х-4)(х-5)(х-6)=0 , если либо (х-4)=0, либо (х-5)=0 , либо (х-6)=0 .
То есть либо х=4 , либо х=5 , либо х=6 .
Значит мы получили три значения переменной "х", при которых левая часть обратиться в 0 . Это и есть корни уравнения.
Проверим, подставим вместо "х" значение 4, получим
(4-4)(4-5)(4-6)=0*(-1)*(-2)=0 .
х=5: (4-5)(5-5)(5-6)=(-1)*0*(-1)=0 ,
х=6: (6-4)(6-5)(6-6)=2*1*0=0 .
ответ: х₁=4 , х₂=5 , х₃=6 .