16
Объяснение:
|x| + |y| = 4 - квадрат с вершинами в точках (0;4), (4;0), (0;-4), (-4;0)
x = 0 => y = 4, y = -4
y = 0 => x = 4, x = -4
x² + y² = a - окружность радиуса
x = 0 => y = , y = -
y = 0 => x = , x = -
Система будет иметь 4 решения, когда окружность и квадрат будут пересекаться в 4х точках => = 4 => a = 4² = 16
16
Объяснение:
|x| + |y| = 4 - квадрат с вершинами в точках (0;4), (4;0), (0;-4), (-4;0)
x = 0 => y = 4, y = -4
y = 0 => x = 4, x = -4
x² + y² = a - окружность радиуса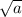
x = 0 => y =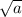 , y = -
, y = -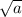
y = 0 => x =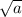 , x = -
, x = -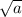
Система будет иметь 4 решения, когда окружность и квадрат будут пересекаться в 4х точках =>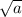 = 4 => a = 4² = 16
= 4 => a = 4² = 16