Так, ну смотрите. Они просто обрезали решение. Если решать подробнее, то получается вот так:
Минус перед первой дробью мы можем поставить в числитель, сути это не поменяет. Приводим слагаемые к общему знаменателю, для этого домножаем второе на :
При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитается числитель второй дроби, а знаменатель остаётся прежним.
Дробь равна нулю тогда, когда её числитель равен нулю, а знаменатель отличен от нуля, этот нюанс в приложенном решении учтён. Приравниваем числитель к нулю:
Так, ну смотрите. Они просто обрезали решение. Если решать подробнее, то получается вот так:
Минус перед первой дробью мы можем поставить в числитель, сути это не поменяет. Приводим слагаемые к общему знаменателю, для этого домножаем второе на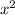 :
:
При вычитании дробей с одинаковыми знаменателями из числителя первой дроби вычитается числитель второй дроби, а знаменатель остаётся прежним.
Дробь равна нулю тогда, когда её числитель равен нулю, а знаменатель отличен от нуля, этот нюанс в приложенном решении учтён. Приравниваем числитель к нулю:
Ну и далее уже как на картинке.
ответ: х= -1/2
Объяснение: 1) ОДЗ: х≠0 ⇒ х = 0 -точка разрыва функции; 2) найдём промежутки возрастания и убывания функции: y'= e^(1/x) · (-1/x²)= - e^(1/x) / x², ⇒ уравнение y'=0 e^(1/x) / x² =0 корней не имеет; y'<0 на (-∞;0) -убывает и y'< 0 на (0; +∞) -убывает. 3) Найдём промежутки вогнутости и выпуклости функции: y'' = 2e^(1/x) /x³ + e^(1/x) /x⁴ = (2x+1) · e^(1/x) /x⁴ ; если y''=0, то (2x+1) · e^(1/x) /x⁴ =0 , ⇒х= -1/2; на (-∞ ;-1/2) y''<0 т.е. функция выпукла; на (-1/2; 0) y''>0 , т.е. функция вогнута ; на (0; +∞) y''>0 , т.е. функция вогнута. Значит х=-1/2 точка перегиба