Чтобы решить эту задачу, нам необходимо узнать, чему равно число размещений из 4 по 3 (иными словами, сколькими можно объединить 4 различных объекта в группы по 3).
Применяем следующую формулу: , где n - общее число объектов (в нашем случае - 4), k - количество объектов в размещении (в нашем случае - 3).
Производим расчеты:
Пояснения:
Факториал числа n (обозначаемый знаком !) - это произведение всех натуральных чисел от 1 до n включительно.
ответ: 24
Чтобы решить эту задачу, нам необходимо узнать, чему равно число размещений из 4 по 3 (иными словами, сколькими можно объединить 4 различных объекта в группы по 3).
Применяем следующую формулу: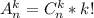 , где n - общее число объектов (в нашем случае - 4), k - количество объектов в размещении (в нашем случае - 3).
, где n - общее число объектов (в нашем случае - 4), k - количество объектов в размещении (в нашем случае - 3).
Производим расчеты:
Пояснения:
Факториал числа n (обозначаемый знаком !) - это произведение всех натуральных чисел от 1 до n включительно.