Пусть х кг - первоначальная масса смеси, тогда
20 : х • 100% = % - процентное содержание чечевицы в первоначальной смеси.
(х+25) кг - масса новой смеси, с добавлением 25кг чечевицы, тогда
(20+25) : (х+25) • 100% = % - процентное содержание чечевицы в новой смеси.
По условию
на 20%
Получаем уравнение:
ОДЗ: x>20
Дробь равна 0, если числитель равен 0, а знаменатель по ОДЗ не равен 0.
Проверка: х = 50 кг
20 : 50 • 100% = 40 % - процентное содержание чечевицы в первоначальной смеси.
45 : (50+25) • 100% = 60% - процентное содержание чечевицы в новой смеси.
60% - 40% = 20% удовлетворяет условию.
ответ: 50 кг
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
Пусть х кг - первоначальная масса смеси, тогда
20 : х • 100% =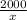
% - процентное содержание чечевицы в первоначальной смеси.
(х+25) кг - масса новой смеси, с добавлением 25кг чечевицы, тогда
(20+25) : (х+25) • 100% =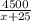
% - процентное содержание чечевицы в новой смеси.
По условию
Получаем уравнение:
ОДЗ: x>20
Дробь равна 0, если числитель равен 0, а знаменатель по ОДЗ не равен 0.
Проверка: х = 50 кг
20 : 50 • 100% = 40 % - процентное содержание чечевицы в первоначальной смеси.
45 : (50+25) • 100% = 60% - процентное содержание чечевицы в новой смеси.
60% - 40% = 20% удовлетворяет условию.
ответ: 50 кг
x2 + 4x + 8 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = 42 - 4·1·8 = 16 - 32 = -16
Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.
4x2 - 12x + 9 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-12)2 - 4·4·9 = 144 - 144 = 0
Так как дискриминант равен нулю то, квадратное уравнение имеет один действительных корень:
x = 122·4 = 1.5
3x2 - 4x - 1 = 0
Найдем дискриминант квадратного уравнения:
D = b2 - 4ac = (-4)2 - 4·3·(-1) = 16 + 12 = 28
Так как дискриминант больше нуля то, квадратное уравнение имеет два действительных корня:
x1 = 4 - √282·3 = 23 - 13√7 ≈ -0.21525043702153024
x2 = 4 + √282·3 = 23 + 13√7 ≈ 1.5485837703548635
2x2 - 9x + 15 = 0 Найдем дискриминант квадратного уравнения: D = b2 - 4ac = (-9)2 - 4·2·15 = 81 - 120 = -39 Так как дискриминант меньше нуля, то уравнение не имеет действительных решений.