Среди решений уравнения x+3y−20=0 найди такую пару, которая состоит из двух таких чисел, первое из которых в 2 раза больше второго.
ответ:
пара чисел: ( ) ; ( )

Рассмотрим первое уравнение:

Можно построить этот график. Учитывая неравенство, строим до прямой x = 6.

Рассмотрим второе уравнение:

График этого уравнения — прямая, проходящая через точку (6; 0) с меняющимся углом наклона. Причём из него же следует, что точку с y = 2 можно выколоть на графике первого уравнения.

График первого уравнения начерчен красным цветом, вариации второго — зелёным.

Возьмём a = 0 и будем увеличивать угол наклона. До a = 1 будет ровно одно пересечение. При a ≥ 1 прямая либо будет параллельна прямой y = x + 2, либо не будет иметь пересечений.

Если уменьшать угол наклона, то при отрицательных a будет два решения, за исключением случаев, когда прямая проходит через выколотую точку (0; 2) и "общую" точку (3; 5):

При (0; 2) При (3; 5)

ответ:

На оси х лежат точки, ордината которых равна 0, поэтому в точке пересечения графиков М(х; 0). Найдем х, решив систему уравнений:
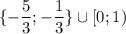
Система:
7х-3у=-21  |*2 <=>  14x-6y=-42 
2х-5у=m    |*7          14x-35y =7m      вычтем из верхнего уравнения нижнее, получим:      0+29y=-42-7m и т.к. у=0, то
                                          42=-7m
                                           -6=m
Проверка:
Cистема:
7х-3у=-21 | * 2     <=>  _14x-6y=-42
2х-5у=-6   | * 7               14x-35y=-42
                                         0 +29y=0
                                                  y=0
=> точка пересечения лежит на оси Х
14х-0=-42
14х=-42
    х=-3  М(-3; 0)