ну я так понимаю, что надо описать алгоритм решения квадратного уравнения. Сначала приведу подобные слагаемые в этом уравнении:
24x² - 10x - 25 = 0
Мы получили полное квадратное уравнение. Далее, нам надо вычислить его дискриминант, и на его основании сделать вывод о наличии корней и их количестве. Если D >0, то уравнение имеет 2 корня, если D = 0, то уравнение имеет 1 корень, если же D<0, то уравнение вообще не имеет корней. Он расчитывается по формуле D = b² - 4ac. подставим, и вычислим D
D = b² - 4ac = 100 + 2400 = 2500 >0, значит, уравнение имеет два различных корня.
Корни тогда вычисляются по следующим формулам:
x1,2 = (-b ± √D) / 2a
Подставим в эту формулу значение D, значение второго и старшего коэффициентов и получим:
1)f'(x)=40x^3-6
2)f'(x)=x+12
3)f'(x)=3cos(x)-sin(x)
4)f'(x)=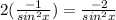
(выводить не буду, это табличная производная)
5) f'(x)=20x^3 -4sin(x)
6)f'(x)=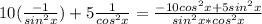
(1)
cos^2x=1-sin^2x
Получаем:
7) f(x)=tgx*(2-3x^3) Представим f(x) как произведение двух функций:
u(x)=tg(x) и v(x)=2-3x^3
По формуле производной от произведения: f(x)=u(x)v(x); f'(x)=u'(x)v(x)+u(x)v'(x)
Теперь вычислим:
Можно конечно упрощать, но я думаю что можно обойтись и без этого
ну я так понимаю, что надо описать алгоритм решения квадратного уравнения. Сначала приведу подобные слагаемые в этом уравнении:
24x² - 10x - 25 = 0
Мы получили полное квадратное уравнение. Далее, нам надо вычислить его дискриминант, и на его основании сделать вывод о наличии корней и их количестве. Если D >0, то уравнение имеет 2 корня, если D = 0, то уравнение имеет 1 корень, если же D<0, то уравнение вообще не имеет корней. Он расчитывается по формуле D = b² - 4ac. подставим, и вычислим D
D = b² - 4ac = 100 + 2400 = 2500 >0, значит, уравнение имеет два различных корня.
Корни тогда вычисляются по следующим формулам:
x1,2 = (-b ± √D) / 2a
Подставим в эту формулу значение D, значение второго и старшего коэффициентов и получим:
x1 = 10 - 50 / 48 = -40/48 = -5/6
x2 = 10 + 50 / 48 = 60/48 = 1.25