Три числа, из которых третье равно 18, образуют геометрическую прогрессию. Если вместо 18 взять число 16, то эти числа составляют арифметическую прогрессию. Найдите эти числа.

А 16 км В

> х км/ч                                ?                           (х + 9) км/ч <

1,5 ч = 90 мин = 90/60 = 3/2 ч

20 мин = 20/60 = 1/3 ч

Уравнение:

х · (3/2 + 1/3) + (х + 9) · 1/3 = 16

3/2х + 1/3х + 1/3х + 9/3 = 16

9/6х + 2/6х + 2/6х + 3 = 16

13/6х = 16 - 3

13/6х = 13

х = 13 : 13/6

х = 13/1 · 6/13

х = 6 (км/ч) - скорость пешехода

6 + 9 = 15 (км/ч) - скорость велосипедиста

ответ: 6 км/ч и 15 км/ч.

Проверка:

6 · (3/2 + 1/3) = 6 · 11/6 = 66/6 = 11 км - пройдёт пешеход за 1 ч 50 мин

15 · 1/3 = 15/3 = 5 км - проедет велосипедист за 20 мин

11 + 5 = 16 км - расстояние между пунктами

Объяснение:

Мы знаем, что помимо положительных чисел, меньше нуля существуют еще и отрицательные числа.

Поэтому, при сложении отрицательного и положительного числа, всегда из положительного числа вычитается отрицательное, то есть, наглядно первый пример можно преобразовать как:

, тогда становится понятнее логика сложения отрицательного с положительным числом.

Второй пример аналогичен первому: если из положительного числа, то есть 3, вычесть отрицательное число, то есть 5, получим как раз -2: .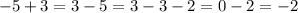

Пойдем ниже, в третьем примере из положительного числа вычитают большее отрицательное число. Поэтому в таких случаях запись можно преобразовать как: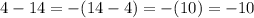 , то есть, мы из отрицательного числа вычитаем положительное число и заносим эту операцию над двумя числами в скобки со знаком "минус".

Четвертый и пятый пример аналогичны первому, когда мы можем представить запись в виде:

То есть, если число со знаком "+" больше числа со знаком "-", мы имеем право переписать запись в виде обычного вычитания из большего числа меньшее, где получим положительное число в ответе.