Войти Регистрация Спроси ai-bota

Тригонометрия, 10 кл.

Тригонометрия, 10 кл.

Показать ответ

Ответ:

Zayka1231

03.09.2020 00:57

‥・Здравствуйте, tima0604! ・‥

• ответ:

Упрощённым выражением данного примера является решение -11+√21. (Альтернативный Вид: ≈ -6,41742.)

• Как и почему?

Для того, чтобы нам проверить правильность нашего ответа, то мы должны делать следующее:

• 1. Упростить корень √12: (√7-2√3)×(√7+3√3).

• 2. Перемножить выражения в скобках, то есть, раскрыть их: 7+3√21-2√21-18.

• 3. Вычислить разность чисел 7 и 18: 7-18=-11 → -11+3√21-2√21.

• 4. Привести подобные члены 3√21 и 2√21: -11+√21.

• Вывод: Таким образом, у нас в ответе получается корень -11+√21, а Альтернативный Вид этого корня является примерно -6,41742.

‥・С уважением, Ваша GraceMiller! :) ・‥

0,0(0 оценок)

Ответ:

Yasmin11111

12.06.2022 19:17

$\boxed{\dfrac{8}{3}}$ квадратных единиц

Объяснение:

Построим график $y = -x^{2} + 4x - 4$

Пусть S площадь ограниченная графиком функции $y = -x^{2} + 4x - 4$ осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.

$y(0) = -0^{2} + 4 * 0 - 4 = -4$

y = 0

$-x^{2} + 4x - 4 = 0|*(-1)$

$x^{2} - 4x + 4 =0$

$(x - 2)^{2} = 0 \Longleftrightarrow x - 2 =0$

x = 2

Координаты точек A и B:

A(0;-4)

B(2;0)

Пусть точка начало системы координат, тогда точка O имеет координаты O(0;0).

Узнаем уравнение прямой проходящей через точки A и B. Уравнение прямой с угловым коэффициентом в общем виде: y = kx + b .

$\displaystyle \left \{ {{A: -4=k * 0 + b} \atop {B:0=2*k + b}} \right.$ $\displaystyle \left \{ {{ b=-4} \atop {0=2k - 4}} \right.$ $\displaystyle \left \{ {{ b=-4} \atop {4=2k |:2}} \right.$ $\displaystyle \left \{ {{ b=-4} \atop {k = 2}} \right.$

y = 2x - 4

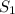Пусть $S_{1}$ - площадь между прямой 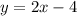y = 2x - 4 и функцией $y = -x^{2} + 4x - 4$

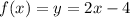Пусть f(x) = y = 2x - 4 и $g(x) = y = -x^{2} + 4x - 4$ .

$S = S_{\bigtriangleup AOB} - S_{1}$

$OA = \sqrt{(x_{A} - x_{O})^{2} + (y_{A} - y_{O})^{2}} = \sqrt{(0 - 0)^{2} + (-4 - 0)^{2}} =\sqrt{16} = 4$

$OB = \sqrt{(x_{B} - x_{O})^{2} + (y_{B} - y_{O})^{2}} = \sqrt{(2 - 0)^{2} + (0 - 0)^{2}} =\sqrt{4} = 2$

По формуле площади прямоугольного треугольника:

$S_{\bigtriangleup AOB} = \dfrac{AO * OB}{2} = \dfrac{4 * 2}{2} = 4$ .

Промежуток интегрирования: [0;2]

Докажем, что $f(x) \geq g(x)$ при $x \in [0;2]$

$2x- 4 \geq -x^{2} + 4x - 4$

$x^{2} - 2x \geq 0$

$x(x - 2) \geq 0$

$x \in (-\infty;0] \cup [2;+\infty)$ тогда можно сделать вывод, что

$g(x) \geq f(x)$ при $x \in [0;2]$ .

По теореме:

$S_{1} = \displaystyle \int\limits^2_0 {(g(x) - f(x))} \, dx = \int\limits^2_0 {-x^{2} +4x - 4 - 2x + 4} \, dx = \int\limits^2_0 {2x-x^{2}} \, dx =$

$= x^{2} - \dfrac{x^{3} }{3} \bigg|_0^2 = (2^{2} - \dfrac{2^{3} }{3}) - 0 = 4 - \dfrac{8}{3} = \dfrac{12 - 8}{3} = \dfrac{4}{3}$ .

$S = S_{\bigtriangleup AOB} - S_{1} = 4 - \dfrac{4}{3} = \dfrac{12 -4}{3} = \dfrac{8}{3}$ квадратных единиц.

найти площадь фигуры,ограниченной осями координат и параболой

найти площадь фигуры,ограниченной осями координат и параболой

найти площадь фигуры,ограниченной осями координат и параболой

0,0(0 оценок)

Популярные вопросы: Алгебра

kholov03

09.09.2021 14:07

На тарілці 5 яблук і 3 груші. скількома з тарілки можна взяти:а)один фрукт; б)одне яблуко та одну грушу?...

daryia210407

06.03.2023 22:35

Отметьте и подпишите на координатной прямой точки A (2 5/14) B (2 8/21) и C (-1.25)...

Mavl58

06.08.2022 08:13

В прямоугольном треугольнике ABC C-90градусов, BC-7 см найти...

ebanat3

06.12.2020 03:28

Записать: 1)удвоенную сумму чисел 5 и m 2)половину разности чисел c и d 3)сумму числа 12 и произведения числа a и b 4)частное от деления суммы чисел n и m на число 17.записать: 66%...

Марьяша16

27.04.2023 11:33

Производительности двух тракторов относятся как . при совместной работе тракторы могут вспахать все поле за 8 часов. работая поочередно, тракторы вспахали все поле. сколько часов проработал...

Тарана11лет9456

27.04.2023 11:33

Решить: 41х-58х+6у-у; -5.1а-4b-4.9а+b; 7.5x+y-8.5x-3.5y...

Макоська

27.04.2023 11:33

Завод по плану должен был изготовить 537000 изделий. план был выполнен на 102,5%. установите: сколько изделий выпустил завод; сколько изделий выпустил завод сверх плана....

Dron133

27.04.2023 11:33

Решите надо надо tg^2(270+a)*sin^2(180+a)...

Ада20000

27.04.2023 11:33

Может ли при каком либо значении a быть равным нулю значение выражения: 1) a+999999 2) 3/a-5 3) a-1/47+a 4) a2 + 1 ?...

Lastivka2016

13.04.2020 22:27

Область значений функции f(x)=-x^2+5...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку