Туындыны табу ережелері көмектесіңдерш​

Y = - 2x + b; уравнение касательной, где угловой коэффициент  k = - 2. 
 y = -4x^2 + 6x; уравнение параболы.
Так как значение производной в точке касания равно значению углового коэффициента касательной, проведенной к графику ф-ции в точке касания, то найдем производную и приравняем ее к минус 2.
 y '(x) = k = - 2;
y '(x) = - 8x + 6;
- 8x + 6 = -2;
- 8x = -8;
 x = 1; это координата точки касания.
Подставим это значение х в формулу ф-ции и найдем ординату точки касания(у).
у(1) = - 4 x^2 + 6x = -4*1^2 + 6*1 = - 4 + 6 = 2.
ответ: ордината точки касания равна 2.

1) х = 0,25

2) х = -5

3) y= -0.6

4) y = -0.75

Объяснение:

1) x(x-4)=2+(x-1)²;

х*х + х*(-4) = 2 + (х-1)(х+1)

- 4х = 2+ х*х + х*1 - 1*х - 1*1

- 4х = 2 + + х - х - 1

-4х - х + х = 2 - 1

-4х = 1

х = 1/4

х = 0,25

2). (x+2)(x-3)-3=(x+1)²

х*х + х*(-3) + 2*х + 2*(-3) = (х+1)(х-1)

- 3х + 2х - 6 = - х + х - 1

-х = 5 (умножить на -1)

х = -5

3)y(5-y)=1-(y+2)²

5у -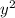 = 1 - (y+2)(y-2)

5y -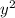 = 1 - 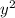- 2y + 2y - 4

5y + 2y -2y = 1-4

5y = -3

y = -3/5

y = -0.6

4) (y-1)²-(y+1)(y-7)=0.​

(y-1)(y+1) -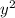 + 7y + y + 7 = 0

+ y - y - 1 - + 7y + y + 7 = 0

8y = -6

y = -6/8

y = -0.75