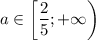Уравнение будет иметь корни, если квадрат синуса принимает значения из отрезка . Но синус не может равняться 0, как было отмечено ранее. Значит, допустимые значения квадрата синуса:
ответ:
Уравнение будет иметь корни, если квадрат синуса принимает значения из отрезка![[0;\ 1]](/tpl/images/1095/0237/b262e.png) . Но синус не может равняться 0, как было отмечено ранее. Значит, допустимые значения квадрата синуса:
. Но синус не может равняться 0, как было отмечено ранее. Значит, допустимые значения квадрата синуса:
ответ: