В клетках «лестницы» расставлены числа 1, 1, 2, 2, 2, 3, 4, 4, 5, 6, так что сумма чисел в каждом столбце, кроме самого левого, на 1 больше, чем в предыдущем. Сколько существует различных расстановок?
Когда график пересекает ось абсцисс в какой-то точке, координаты этой точки (х;0), все точки лежащие на оси х имеют координату "ноль" по оси у. В итоге можем представить выражение следующим образом:
ответ: 1.
2)
Опять же в точке пересечения графика с абсциссой координаты по оси у это 0, значит:
ответ: 2 и -14.
3)
1) Можно раскрыть модуль по определению и увидеть, что получиться, а можно подумать. Есть какая-то функция, которая преобразует х в у (у=х), и отрицательные и положительные значения. А если взять модуль от х, то функция будет принимать те же значения для отрицательных значениях х, что и для положительных (когда они равны по модулю, пример -2 и 2), получается когда х будет отрицательным значения по оси х будут такими же, проще говоря всё чтобы справа (когда х положительный), отзеркалится влево по оси у. Покажу пример и другие графики внизу. То есть нам надо отразить график у=х как было сказано выше.
2) Тут уже по определению, но и всё просто:
Два линейных уравнения.
4)
Если что-то пересекается в одной точке на координатной плоскости, то у них есть общие точки, то есть существует такая точка M--> (x₀;y₀), которая подходит есть в любой из функций, которые пересекаются в этой точке.
Теперь построение на общей координатной плоскости
Первая функция: Получили точки пересечения с осью у и х соответственно.
Английский язык
Преобразуйте слова, если это необходимо, так, чтобы они грамматически соответствовали содержанию текста.
Ladoga
Have you ever been to Ladoga? It is a small villag...
.Функция задана формулой f (х) = х2/5 – 6х. Найдите: 1) f (5) и f (–1); 2) нули функции. 2.Найдите область определения функции f (х) = (х + 6)/(х2 – 3 х – 4)
3.Постройте график функции f (х) = х2 – 8х +7.
Используя график, найдите:
1) область значений функции;
2) промежуток возрастания функции;
3) множество решений неравенства f (x) > 0.
34Постройте график функции: 1) f (х) = √х + 2; 2) f (х) = √[х + 2].
5.Найдите область определения функции f (х) = √[x + 3] + 8/(х2 – 36).
6.При каких значениях b и c вершина параболы у = –4х2 + bx + c находится в точке A (3; 1)?
Решите Очень вас! Желательно с полным расписанием действий и вычеслений!
1)
Когда график пересекает ось абсцисс в какой-то точке, координаты этой точки (х;0), все точки лежащие на оси х имеют координату "ноль" по оси у. В итоге можем представить выражение следующим образом:
ответ: 1.
2)
Опять же в точке пересечения графика с абсциссой координаты по оси у это 0, значит: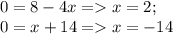
ответ: 2 и -14.
3)
1) Можно раскрыть модуль по определению и увидеть, что получиться, а можно подумать. Есть какая-то функция, которая преобразует х в у (у=х), и отрицательные и положительные значения. А если взять модуль от х, то функция будет принимать те же значения для отрицательных значениях х, что и для положительных (когда они равны по модулю, пример -2 и 2), получается когда х будет отрицательным значения по оси х будут такими же, проще говоря всё чтобы справа (когда х положительный), отзеркалится влево по оси у. Покажу пример и другие графики внизу. То есть нам надо отразить график у=х как было сказано выше.
2) Тут уже по определению, но и всё просто:
Два линейных уравнения.
4)
Если что-то пересекается в одной точке на координатной плоскости, то у них есть общие точки, то есть существует такая точка M--> (x₀;y₀), которая подходит есть в любой из функций, которые пересекаются в этой точке.
Теперь построение на общей координатной плоскости
Первая функция: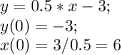
Получили точки пересечения с осью у и х соответственно.
Вторая функция: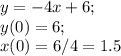
Третья функция: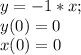
ответ: -1.
Преобразуйте слова, если это необходимо, так, чтобы они грамматически соответствовали содержанию текста.
Ladoga
Have you ever been to Ladoga? It is a small villag...
.Функция задана формулой f (х) = х2/5 – 6х. Найдите: 1) f (5) и f (–1); 2) нули функции. 2.Найдите область определения функции f (х) = (х + 6)/(х2 – 3 х – 4)
3.Постройте график функции f (х) = х2 – 8х +7.
Используя график, найдите:
1) область значений функции;
2) промежуток возрастания функции;
3) множество решений неравенства f (x) > 0.
34Постройте график функции: 1) f (х) = √х + 2; 2) f (х) = √[х + 2].
5.Найдите область определения функции f (х) = √[x + 3] + 8/(х2 – 36).
6.При каких значениях b и c вершина параболы у = –4х2 + bx + c находится в точке A (3; 1)?
Решите Очень вас! Желательно с полным расписанием действий и вычеслений!