В первой вазе — 7 яблок(-а), во второй — 5 груш(-и), в третьей — 9 апельсин(-ов, -а). Случайно берётся один фрукт из любой вазы. Вычисли, сколькими различными это можно сделать.
ответ - первый случай: во сколько раз увеличим скорость, во столько же раз уменьшим время движения.
Второй случай не относится ни к обратной, ни даже к прямой пропорциональности.
Третий случай - это прямая пропорциональность.
P.s. Но хочу уточнить - если бы в третьем случае нам было сказано, что у нас есть фиксированная сумма денег, которую надо потратить на этот товар, то это тоже была бы обратная пропорциональность - при увеличении цены во сколько-то раз количество купленного товара во столько же раз уменьшилось бы.
Тангенс наклона касательной, вида y=kx+b, к графику у=f(x), с абсциссой x₀ у точки касания, равен f'(x₀): tgα=k=f'(x₀).
f(x)=2x³-3x²-4; y=12x+1
Прямые вида y=kx+b параллельны, если k - одинаковый коэффициент. Откуда 12=k=f'(x₀).
f'(x) = (2x³)'-(3x²)'-4' = 6x²-6x
f'(x₀) =
Осталось проверить, что y=12x+1 не является касательной к y=f(x) т.к. эта прямая должна быть параллельна касательной, а не совпадать с ней.
12x+1 = 2x³-3x²-4
2x³-3x²-12x-5 = 0
x²(2x+1) - 2x(2x+1) - 5(2x+1) = 0
(2x+1)(x²-2x-5) = 0
x=-0,5 или x²-2x-5=0, D=(-2)²-4·(-5) = 24 > 0 ⇒ уравнение имеет 3 решения, поэтому y=12x+1 не касается y=f(x). В данном случаи при касании было бы 2 решения.
ответ - первый случай: во сколько раз увеличим скорость, во столько же раз уменьшим время движения.
Второй случай не относится ни к обратной, ни даже к прямой пропорциональности.
Третий случай - это прямая пропорциональность.
P.s. Но хочу уточнить - если бы в третьем случае нам было сказано, что у нас есть фиксированная сумма денег, которую надо потратить на этот товар, то это тоже была бы обратная пропорциональность - при увеличении цены во сколько-то раз количество купленного товара во столько же раз уменьшилось бы.
Тангенс наклона касательной, вида y=kx+b, к графику у=f(x), с абсциссой x₀ у точки касания, равен f'(x₀): tgα=k=f'(x₀).
f(x)=2x³-3x²-4; y=12x+1
Прямые вида y=kx+b параллельны, если k - одинаковый коэффициент. Откуда 12=k=f'(x₀).
f'(x) = (2x³)'-(3x²)'-4' = 6x²-6x
f'(x₀) =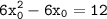
Осталось проверить, что y=12x+1 не является касательной к y=f(x) т.к. эта прямая должна быть параллельна касательной, а не совпадать с ней.
12x+1 = 2x³-3x²-4
2x³-3x²-12x-5 = 0
x²(2x+1) - 2x(2x+1) - 5(2x+1) = 0
(2x+1)(x²-2x-5) = 0
x=-0,5 или x²-2x-5=0, D=(-2)²-4·(-5) = 24 > 0 ⇒ уравнение имеет 3 решения, поэтому y=12x+1 не касается y=f(x). В данном случаи при касании было бы 2 решения.
ответ: х = {-1;2}.