В равнобедренном треугольнике DBP проведена биссектриса PM угла P у основания DP, ∡ PMB = 126°. Определи величины углов данного треугольника (если это необходимо, промежуточные вычисления и ответ округли до тысячных).
Вероятность по классической формуле равна: где A - событие; P(A) - вероятность этого события; n - общее количество событий , а m - количество событий, которые событию A.
1) Сначала найдём общее количество исходов n - это число выбрать наудачу любые 5 деталей из 12 имеющихся. Несомненно, что если я в правой руке буду держать 3 детали, а в правой - 2, или наоборот, то результат того, когда мы взяли в руки детали и как именно, будет несущественным. Поэтому число всех исходов .
2) Перейдем теперь к число событиям событию A (т.е. к m). Чтобы число m благоприятсвовало событию A, нужно чтобы из 5 наудачу взятых деталей 2 были стандартными, а 3 - нестандартных.
Стандартных деталей всего 9, а число выбрать из 9 стандартных деталей только 2 (стандартных) равно .
Нестандартных деталей всего , а число выбрать из 3 нестандартных те же 3 нестандартных равно .
3) Если первое действие можно выполнить а второе действие то все действия могут быть выполнены правило умножения). Пусть первое действие это выбирание 2 стандартных деталей из 9 (), а второе действие - выбирание 3 нестандартных деталей из 3 (), тогда всего выбрать 2 стандартные детали из 9 и 3 нестандартные детали из 3 будет:
Объяснение:
Вероятность по классической формуле равна: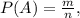 где A - событие; P(A) - вероятность этого события; n - общее количество событий , а m - количество событий, которые событию A.
где A - событие; P(A) - вероятность этого события; n - общее количество событий , а m - количество событий, которые событию A.
1) Сначала найдём общее количество исходов n - это число выбрать наудачу любые 5 деталей из 12 имеющихся. Несомненно, что если я в правой руке буду держать 3 детали, а в правой - 2, или наоборот, то результат того, когда мы взяли в руки детали и как именно, будет несущественным. Поэтому число всех исходов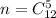 .
.
2) Перейдем теперь к число событиям событию A (т.е. к m). Чтобы число m благоприятсвовало событию A, нужно чтобы из 5 наудачу взятых деталей 2 были стандартными, а 3 - нестандартных.
Стандартных деталей всего 9, а число выбрать из 9 стандартных деталей только 2 (стандартных) равно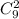 .
.
Нестандартных деталей всего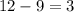 , а число выбрать из 3 нестандартных те же 3 нестандартных равно
, а число выбрать из 3 нестандартных те же 3 нестандартных равно 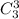 .
.
3) Если первое действие можно выполнить а второе действие то все действия могут быть выполнены правило умножения). Пусть первое действие это выбирание 2 стандартных деталей из 9 (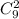 ), а второе действие - выбирание 3 нестандартных деталей из 3 (
), а второе действие - выбирание 3 нестандартных деталей из 3 (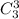 ), тогда всего выбрать 2 стандартные детали из 9 и 3 нестандартные детали из 3 будет:
), тогда всего выбрать 2 стандартные детали из 9 и 3 нестандартные детали из 3 будет: 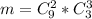
4) Тогда искомая вероятность равна:
Координаты точки пересечения графиков данных функций (4; 2).
Объяснение:
График функции у=8/х гипербола, придаём значения х, вычисляем у, записываем в таблицу.
Таблица:
х -8 -4 -2 -1 0 1 2 4 8
у -1 -2 -4 -8 - 8 4 2 1
График функции у=√х представляет из себя "половинку" параболы, с вершиной в начале координат, как бы "лежащей на боку" на оси Ох.
Также придаём значения х, вычисляем у, записываем в таблицу.
(взяла только целые значения, чтобы легче строить).
Таблица:
х 0 1 4 9
у 0 1 2 3
И из таблиц, и по графику видно, что координаты точки пересечения графиков данных функций (4; 2).