В упражнениях 5.32-5.35, 5.39-5.41 решите неравенства. Н.
5.32. 1) x2 <9;
2) х? >4;
3) (3x – 5)2 < 1;
4) (2 - 5x)?>16;
5) (х - 7 +1> 0;
6) 49 - (3x + 2)2 >0.
даю ​

4 пули 4 выстрела

P1(A)=0.6               P(т)=1-0.6=0.4

P2(тA)=0.6*0.4=0.24

P3(ттA)=0.6*0.4^2=0.096

P4(ttt)=0.4^3=0.064

Складываем вероятности

0.064+0.096+0.24+0.6=1

Х       1       2       3             4

Р    0.6   0.24   0.096   0.063

С монетой все проще. У монеты две стороны. Вероятность того, что монета упадет на ребро столь мала, что это не берется в расчет и целые доли округляются в борльшую сторону, то есть 0.5, так как орел только с одной стороны, бросаем монету один раз, следовательно и шанс 1 из 2, то есть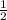 , то есть 0.5

Х      0    1

Р    0.5  0.5

Cторона развертки цилиндра равна корню квадратному из половины квадрата диагонали и равна корню из (4π²:2)= π√2 

Площадь полной пов-сти цилиндра равна площади его боковой поверхности плюс площадь 2х его оснований. 

Чтобы найти площадь основания, нужно знать его радиус. Его найти из длины окружности основания, которая равна стороне развертки цилиндра, т. е. стороне квадрата. 

2πr = π√2см 

r= π√2:2π= 0,5см 

Площадь двух оснований равна 

2πr²= 2*π*0,25= 0,5 π см² 

Площадь боковой пов-сти равна (π√2)²=2π² 

Площадь полной пов-сти цилиндра равна 2π²+0,5 π=0,5π(4π+1)