Вичислить косинус угла между векторами вектор c {1; 1; -1} вектор d {3; -2; 0}

Наибольшее значение функции: мы проводим перпендикуляр от самой верхней точки графика на ось У. Видим, что единица занимает у нас 2 клетки, то есть каждая клетка вверх прибавляет к значению функции по 0,5. У нас перпендикуляр проведен от верхней точки до седьмой клетки. 0,5*7=3,5.

Наименьшее значение функции: проводим перпендикуляр от самой нижней точки графика на ось У. Судя по всему функция монотонно (то есть все время и непрерывно) убывает. Следовательно фактическое наименьшее значение функции мы найти не можем, но можем указать, какое наименьшее значение она принимает на данном графике: выбираем самую нижнюю точку, ведем перпендикуляр до оси У. Это 9 клеток = - 4,5.

Промежутки возрастания: это когда функция идет вверх, простыми словами. Но перпендикуляры мы уже опускаем на ось Х. На нашем графике функция начинается с 6 клетки влево (подняли перпендикуляр от самой нижней точки слева на ось Х), видим, что единица по оси Х - это 2 клетки, значит, 1 клетка = 1/2 = 0,5.

Таким образом, начало функции она берет при Х=-0,5*6 = -3

Растет она до 2 клетки по оси Х. Мы знаем, что 2 клетки - это единица. Она слева от оси, значит, с минусом. Значит, промежуток возрастания = [-3;-1]

Промежутки убывания: Делаем все то же самое (опускаем перпендикуляр на ось Х) только оттуда, где график функции идет вниз.

Мы закончили возрастать на точке -1, дальше она начала падать.

Следовательно промежуток убывания функции от {-1; 5.5}, 5.5 - последний перпендикуляр данного графика на ось Х.

Значения Х, при котором значения функции меньше либо равны 0:

Мы опускаем перпендикуляры на ось Х из тех точек, что меньше 0 по оси У. Первая точка (самая левая), она ниже оси ОХ, значит, нам подходит. Это как мы знаем 6 клетка на ОХ, то есть -3. График пересекает ось ОХ в точке, где Х = где-то -2,2. А дальше функция уже становится больше 0.

Дальше нам не подходит, следовательно первый промежуток: [-3:-2.2}

А второй промежуток, где график функции опускается ниже оси ОХ - это {1,75; 5.5] (напомню, перпендикуляры опускаем на ось ОХ).

квадратных единиц

Объяснение:

Построим график

Пусть S площадь ограниченная графиком функции    осями координат. Пусть точка B - пересечение графика y и оси абсцисс, точка A - пересечение графика y и оси ординат.

Координаты точек A и B:

A(0;-4)

B(2;0)

Пусть точка начало системы координат, тогда точка O имеет координаты O(0;0).

Узнаем уравнение прямой проходящей через точки A и B. Уравнение прямой с угловым коэффициентом в общем виде: .

Пусть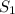 - площадь между прямой 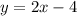и функцией

Пусть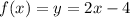 и .

По формуле площади прямоугольного треугольника:

.

Промежуток интегрирования:

Докажем, что при

тогда можно сделать вывод, что

при .

По теореме:

.

квадратных единиц.