421/20
Объяснение:
Имеем Подставим данные выражения в подынтегральное и будем интегрировать по направлению x от 1 до 4:
421/20
Объяснение:
Имеем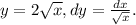 Подставим данные выражения в подынтегральное и будем интегрировать по направлению x от 1 до 4:
Подставим данные выражения в подынтегральное и будем интегрировать по направлению x от 1 до 4: