Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
А
Английский язык
Х
Химия
Э
Экономика
П
Право
И
Информатика
У
Українська мова
Қ
Қазақ тiлi
О
ОБЖ
Н
Немецкий язык
Б
Беларуская мова
У
Українська література
М
Музыка
П
Психология
А
Алгебра
Л
Литература
Б
Биология
М
МХК
О
Окружающий мир
О
Обществознание
И
История
Г
Геометрия
Ф
Французский язык
Ф
Физика
Д
Другие предметы
Р
Русский язык
Г
География
Показать больше
Показать меньше
nastyyya4
19.09.2022 07:43 •
Алгебра
Вычислить площадь фигуры, ограниченной линиями: у=х2-4х+6; у=1; х=1; х=3
Показать ответ
Ответ:
Darkparadise02
15.10.2020 13:10
Решение:
Вспомним формулу Ньютона-Лейбница:
Следуя этой формуле найдём определённый интеграл:
ответ:
0,0
(0 оценок)
Популярные вопросы: Алгебра
AzilotikGame
05.03.2021 16:18
Решите полные квадратные уравнения. 7х=6х^2-5 13х-14-3х^2=0 12=11х+5х^2...
lissden7
05.03.2021 16:18
Икс два минус игрик равно минус двум два икс плюс игрик равно двум...
lana770
05.03.2021 16:18
Докажите что при любом натуральном n значение выражения (9n-4)(9n+-2)(4n+3)+5(6n+9) делится нацело на 7...
ezdinaa
05.03.2021 16:18
Найдите корни уравнения дробь х-4 деленная на х-5 прибавить х-6 деленная на х-5 равно 2...
lcjewfyjozo075
02.11.2022 02:13
Разложите на множители: а)5x²y + 15xy² б) 121а - а³....
Victor111111111
24.12.2020 19:51
Обьясните, какие углы называются внутренними односторонними, внутренними накрест лежащими и соответственными. приз только кратко и слочно...
RL228
09.02.2022 13:56
За 11 тетрадей и 8 ручек заплатили 49 рублей. сколько стоит 1 тетрадь и сколько 1 ручка, если 5 тетрадей дороже 4 ручек на 7 рублей....
arina522
09.03.2023 13:42
Постройте график уравнения: 3х+2у=6....
Brokenheart94
08.05.2022 09:54
Выберите молекулу, у которой химическая связь полярнаяковалентная, но молекула неполярна.А) хлористый водородВ) водаC) аммиакD) оксид углерода (IV)E) сероводород...
Yaniks02
30.10.2020 05:32
алгебра 7 класс номер 6.45. Реши уравнение: 1) х/4+ х/3=7 2) 2х/5+ х/2=3 3) 5х/4- х/2 4) 4х/5 -х/10=7 5) 3х/4+5х/6=38 6) 2х/3+5х надо ...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Вспомним формулу Ньютона-Лейбница: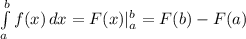
Следуя этой формуле найдём определённый интеграл:
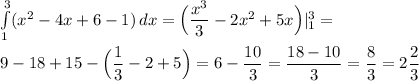
ответ: