Зависимость "двузначному числу ставится в соответствие сумма его цифр" является функциональной, так как каждое двузначное число имеет ровно одну сумму своих цифр.
Найдем требуемые значения:
Значения и найти невозможно, так как зависимость сформулирована лишь для двузначных чисел.
Область определения опять же вытекает из сформулированной зависимости: это все двузначные числа. Записать это можно так:
Найдем область значений. Во-первых, отметим, что сумма цифр двузначного числа по смыслу - это натуральное число. Далее, минимальную сумму цифр среди двузначных чисел имеет число 10 (сумма равна 1), а максимальную - число 99 (сумма равна 18). Можно показать, что все без исключения суммы от 1 до 18 могут быть получены на примере цепочки чисел:
3)x=
4)x=
Объяснение:
3)
Умножаем обе части():
3(6x-1)-4(3x+1)=3
Распределить 3 и 4 через скобки:
18x-3-4(3x+1)=3
18x-3- 12x - 4=3
Привести подобные члены:
6x-3-4=3
6x-7=3
Переносим постоянную(-7) в правую часть и сменяем ее знак:
6x=3+7
Вычисляем:
6x=10
Разделим обе стороны на 6:
x=
4)
Раскрываем скобки:
Умножаем обе части уравнения на 4:
2(2x-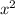 )+3x+2
)+3x+2
Распределяем 2 через скобки(2(2x-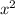 )):
)):
4x-2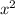 +3x+2
+3x+2
Поскольку сумма двух противоположных величин равна нулю, надо удалить их из выражения(-2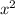 и 2
и 2
4x+3x=4
7x=4
Разделить обе стороны на 7:
x=
Надеюсь
:)
Зависимость "двузначному числу ставится в соответствие сумма его цифр" является функциональной, так как каждое двузначное число имеет ровно одну сумму своих цифр.
Найдем требуемые значения:
Значения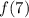 и
и 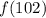 найти невозможно, так как зависимость сформулирована лишь для двузначных чисел.
найти невозможно, так как зависимость сформулирована лишь для двузначных чисел.
Область определения опять же вытекает из сформулированной зависимости: это все двузначные числа. Записать это можно так:
Найдем область значений. Во-первых, отметим, что сумма цифр двузначного числа по смыслу - это натуральное число. Далее, минимальную сумму цифр среди двузначных чисел имеет число 10 (сумма равна 1), а максимальную - число 99 (сумма равна 18). Можно показать, что все без исключения суммы от 1 до 18 могут быть получены на примере цепочки чисел:
10, 11, 12, ..., 18, 19, 29, 39, ..., 89, 99.
Таким образом, область значений: