Выполните умножение и решите уравнение (x-2)(x + 4) + (x-4)(x+ 5) = 2x^{2}-5.

Напишите полное решение.Выполните умножение и решите уравнение (x-2)(x + 4) + (x-4)(x+ 5) = 2x^{2}-5.

Напишите полное решение.

Показать ответ

Ответ:

maxim199431

05.10.2022 16:09

В решении.

Объяснение:

1) [(a-2)/(a+2) - (a+2)/(a-2)] : 12a²/(4-a²)= 2/3а;

a) (a-2)/(a+2) - (a+2)/(a-2)=

общий знаменатель (a+2)(a-2), надписываем над числителями дополнительные множители:

=[(a-2)*(a-2) - (a+2)/(a+2)] / (a+2)/(a-2)=

=[(a-2)² - (a+2)²] / (a+2)/(a-2)=

=[(a²-4a+4) - (a²+4a+4)] / (a+2)/(a-2)=

=(a²-4a+4 - a²-4a-4) / (a+2)/(a-2)=

= -8a / (a+2)/(a-2)=

= -8a / (a²-4);

б) [-8a / (a²-4)] : [12a²/(4-a²)]=

= [-8a / (a²-4)] : [12a²/ -(a²-4)]=

= [ -8a / (a²-4)] : [-12a²/ (a²-4)]=

= [ 8a * (a²-4)] / [(a²-4) * 12a²]=

сократить (разделить) 8а и 12а² на 4а, (a²-4) и (a²-4) на (a²-4):

= 2/3а;

2) [8x/(x-2) + 2x] : [(4x+8)/(7x-14)]= 7х/2;

a) 8x/(x-2) + 2x=

общий знаменатель (x-2), надписываем над числом дополнительный множитель:

= [8х + (x-2)*2х] / (x-2)=

=(8x+2x²-4x) / (x-2)=

=(4x+2x²) / (x-2)=

= [2x(2+x)] / (x-2);

б) [[2x(2+x)] / (x-2)] : [(4x+8)/(7x-14)]=

=[[2x(2+x)] / (x-2)] : [4(x+2)/7(x-2)]=

=[2x(2+x) * 7(x-2)] / [(x-2) * 4(x+2)]=

сократить (разделить) 2 и 4 на 2, (x-2) и (x-2) на (x-2), (x+2) и (x+2) на (x+2):

= 7х/2;

3) 5а/(а+3) + (а-6)/(3а+9) * 135/(6а-а²)= 5(а-3)/а.

а) [(а-6)/(3а+9)] * [135/(6а-а²)]=

=[(а-6)/3(а+3)] * [135/ -а(а-6)]=

=[(а-6) * 135] / [3(а+3) * -а(а-6)]=

сократить 135 и 3 на 3, (а-6) и (а-6) на (а-6):

= -45/а(а+3);

б) 5а/(а+3) + [-45/а(а+3)]=

=5а/(а+3) - (45/а(а+3)=

общий знаменатель а(а+3):

=(а*5а - 45) / а(а+3)=

=(5а²-45) / а(а+3)=

=[5(a²-9)] / а(а+3)=

=[5(a-3)(a+3)] / а(а+3)=

сократить (а+3) и (а+3) на (а+3):

= 5(а-3)/а.

0,0(0 оценок)

Ответ:

ankateren

22.10.2022 19:34

Решение:

Немного теории. Систему уравнений можно записать в следующем виде:

A·x = b

где A - матрица коэффициентов, x - вектор-столбец переменных, b - вектор-столбец свободных членов.

Умножим эту систему на обратную матрицу коэффициентов A⁻¹ слева. Тогда:

A⁻¹·A·x = A⁻¹·b

x = A⁻¹·b

Таким образом, чтобы решить систему уравнений, нужно найти обратную матрицу коэффициентов и умножить ее на вектор-столбец свободных членов.

1) Обратная матрица

Будем искать обратную матрицу через алгебраические дополнения. Для начала найдем определитель матрицы A :

$\Delta =\left|\begin{array}{ccc}2&-1&-2\\3&2&1\\2&3&3\end{array}\right|=2\cdot \left|\begin{array}{cc}2&1\\3&3\end{array}\right|-(-1)\cdot \left|\begin{array}{cc}3&1\\2&3\end{array}\right|+(-2)\cdot \left|\begin{array}{cc}3&2\\2&3\end{array}\right|=\\\\=2\cdot(2\cdot3-3\cdot1)+1\cdot(3\cdot3-2\cdot1)-2\cdot(3\cdot3-2\cdot2)=\\\\=2\cdot(6-3)+1\cdot(9-2)-2\cdot(9-4)=6+7-10=3$

Найдем элементы матрицы алгебраических дополнений:

$A_{11}^{*}=(-1)^{1+1}\cdot \left|\begin{array}{cc}2&1\\3&3\\\end{array}\right|=2\cdot3-3\cdot1=6-3=3$

$A_{12}^{*}=(-1)^{1+2}\cdot \left|\begin{array}{cc}3&1\\2&3\\\end{array}\right|=-(3\cdot3-2\cdot1)=-9+2=-7$

$A_{13}^{*}=(-1)^{1+3}\cdot \left|\begin{array}{cc}3&2\\2&3\\\end{array}\right|=3\cdot3-2\cdot2=9-4=5$

$A_{21}^{*}=(-1)^{2+1}\cdot \left|\begin{array}{cc}-1&-2\\3&3\\\end{array}\right|=-((-1)\cdot3-3\cdot(-2))=3-6=-3$

$A_{22}^{*}=(-1)^{2+2}\cdot \left|\begin{array}{cc}2&-2\\2&3\\\end{array}\right|=2\cdot3-2\cdot(-2)=6+4=10$

$A_{23}^{*}=(-1)^{2+3}\cdot \left|\begin{array}{cc}2&-1\\2&3\\\end{array}\right|=-(2\cdot3-2\cdot(-1))=-6-2=-8$

$A_{31}^{*}=(-1)^{3+1}\cdot \left|\begin{array}{cc}-1&-2\\2&1\\\end{array}\right|=(-1)\cdot1-2\cdot(-2)=-1+4=3$

$A_{32}^{*}=(-1)^{3+2}\cdot \left|\begin{array}{cc}2&-2\\3&1\\\end{array}\right|=-(2\cdot1-3\cdot(-2))=-2-6=-8$

$A_{33}^{*}=(-1)^{3+3}\cdot \left|\begin{array}{cc}2&-1\\3&2\\\end{array}\right|=2\cdot2-3\cdot(-1)=4+3=7$

Тогда:

$A^*=\left(\begin{array}{ccc}3&-7&5\\-3&10&-8\\3&-8&7\end{array}\right)$

Транспонированная матрица алгебраических дополнений:

$(A^*)^T=\left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

Обратная матрица:

$A^{-1}=\frac{1}{\Delta} \cdot (A^*)^T$

$A^{-1}=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

2) Вектор-столбец переменных

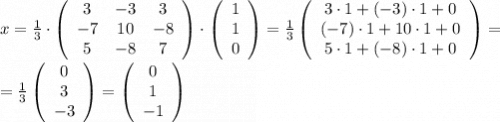
$x=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)\cdot\left(\begin{array}{ccc}1\\1\\0\end{array}\right)=\frac{1}{3} \left(\begin{array}{ccc}3\cdot1+(-3)\cdot1+0\\(-7)\cdot1+10\cdot1+0\\5\cdot1+(-8)\cdot1+0\end{array}\right)=\\\\=\frac{1}{3} \left(\begin{array}{ccc}0\\3\\-3\end{array}\right)=\left(\begin{array}{ccc}0\\1\\-1\end{array}\right)$