Алгебра: Вывести производную косинуса и тангенса.

Покажем, что (cos x) =-sin x По определению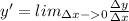 Приращение функции равно Ищем отношение Перейдем в этом равенстве к границе, когда . В следствии непрерывности функции sin x Для второго множителя (используя один из замечательных пределов), обозначив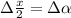 , имеем Поєтому Т.е. (сos x) =-sinx Производная тангенса. Возьмем любую точку х є (a;b), где (a;b) - один из интервалов, на котором определена функция tg x. Ищем приращение Получаем отношение переходим к границе, когда . Следовательно производная...

Вывести производную косинуса и тангенса.

Показать ответ

Ответ:

inzhu123345

25.05.2020 16:14

Покажем, что (cos x)'=-sin x

По определению $y'=lim_{\Delta x-0} \frac {\Delta y}{\Delta x}$

Приращение функции равно

$\Delta y=cos (x+\Delta x)-cos x=-2sin(x+\frac{\Delta x}{2})sin (\frac {\Delta x}{2})$

Ищем отношение

$\frac {\Delta y}{\Delta x}=-sin(x+\frac{\Delta x}{2})\frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}}$

Перейдем в этом равенстве к границе, когда $\Delta x-0$ . В следствии непрерывности функции sin x

$lim_{\Delta x-0} -sin(x+\frac{\Delta x}{2})=- -sin lim_{\Delta x-0}(x+\frac{\Delta x}{2})=-sin x$

Для второго множителя (используя один из замечательных пределов), обозначив $\Delta \frac {x}{2} =\Delta \alpha$ , имеем

$lim_{\Delta x-0} \frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}}= lim_{\alpha-0} \frac {sin \alpha}{\alpha}=1$

Поєтому

$lim_{\Delta x-0} \frac {\Delta y}{\Delta x}=lim_{\Delta x-0} (-sin(x+\frac{\Delta x}{2})\frac {sin (\frac {\Delta x}{2})}{\Delta \frac{x}{2}})=-sin x *1=-sin x$

Т.е. (сos x)'=-sinx

Производная тангенса. Возьмем любую точку х є (a;b), где (a;b) - один из интервалов, на котором определена функция tg x. Ищем приращение

$\Delta y=\frac {sin (x+\Delta x)}{cos(x+\Delta x)}-\frac {sin x}{cos x}= =\frac{sin(x+\Delta x)cos x-sinx cos(x+\Delta x)}{cos(x+\Delta x)cos x}= \frac{sin \Delta x}{cos(x+\Delta x)cos x}$