Задачи: 1. Один из катетов прямоугольного треугольника в три раза больше другого, а его площадь равна 6 кв. см. Найти меньший катет.
2. В треугольнике известны две стороны: 12 см и 16 см, а высоты, проведенные к ним 8 см и 6 см. Найти площадь.
3. Однаиздиагоналейромба12см,аплощадь120кв.см.Найтивторуюдиагональ
4. В равнобокой трапеции основания 2 см и 8 см, а боковая сторона 12 см.
Известно, что острый угол этой трапеции 30 гр. Найти площадь.
5. 10сми15см,авысота,проведеннаякбольшей
из них равна 6 см. Найти вторую высоту.
6. В Прямоугольном треугольнике один из углов равен 60 гр, а противолежащий к
нему катет 10 см. Найдите площадь, если гипотенуза 18 см.
7. 30гр.,АВ=14см,ВС=10см.Найтиплощадь. 8. Диагонали ромба относятся как 2:3, а его площадь 48 кв. см. Найдите большую
диагональ.
9. Найдите площадь фигуры на клетчатой бумаге, считая сторону клетки равной 1.
10.Найдите площадь фигуры на клетчатой бумаге, считая сторону клетки равной 1.
11.Найдите площадь фигуры на клетчатой бумаге, считая сторону клетки равной 1.
12.Найдите площадь фигуры на клетчатой бумаге, считая сторону клетки равной 1.
нушно

1) 3

2) 1,5

3) 2/3

4) -0,9

5) 1

Объяснение:

1)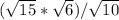 = = 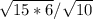= = 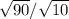= 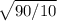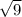3

знак "/" - дробь; сначала я поставила числитель под один знак корня и перемножила числа, потом поставила все уравнение под знак корня, разделила 90 на 10 и получила 9. корень из 9 = 3

2)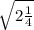 = = 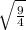= = 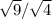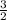1.5

перевела дробь в неправильную (2 умножила на 4 и прибавила 1), получила 9/4. Поставила числитель и знаменатель отдельно под знак корня. Выразила из под корня 9 и 4. и получила 3/2.

3) = = =

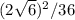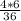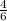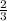
возвела скобку в степень. 2 поставила в квадрат. корень из 6 в квадрате равен подкоренному выражению (с любым числом под корнем получится число из под корня). получили 4 и 6. умножаем, сокращаем, получаем 4/6 или 2/3

4) = =

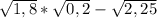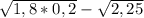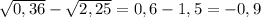
ставим 1,8 и 0,2 под один корень, перемножаем, получаем 0,36. выводим число из под корня. получаем 0,6 и 1,5, вычитаем, получаем -0,9

5)

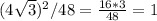
делаем то же самое, что и в 3 примере. 16 * 3 = 48

число, деленное само на себя ровно 1

В решении.

Объяснение:

Дана функция у=√х:  

а) График которой проходит через точку с координатами А(а; 83). Найдите значение а.  

Нужно в уравнение подставить известные значения х и у (координаты точки А):  

83 = √а  

(83)² = (√а)²  

а=6889;  

b) Если х∈[0; 36], то какие значения будет принимать данная функция?  

у= √х  

у=√0=0;  

у=√36=6;  

При х∈ [0; 36]   у∈ [0; 6].  

с) y∈ [14; 28]. Найдите значение аргумента.  

14 = √х  

(14)² = (√х)²  

х=196;  

28 = √х  

(28)² = (√х)²  

х=784;  

При х∈ [196; 784]   y∈ [14; 28].  

d) Найдите при каких х выполняется неравенство у ≤ 5.  

√х <= 5  

(√х)² <= (5)²  

х <= 25;  

Неравенство у ≤ 5 выполняется при х <= 25.