Задание 1: а) Составьте таблицы значений для функций у = х2, у = 2х2, у = 0,5х2.
б) Постройте графики данных функций.
в) Можно ли получить графики функций у = 2х2 и у = 0,5х2, изменяя график функции у = х2.

Построим график квадратной функции методом "по 3 точкам", а именно по вершине параболы и двум её корням (дискриминант не отрицательный).

Это координаты вершины, почему именно такие? Корни уравнения:

, функция чётная (есть ось симметрии), и есть какая координата по оси Ох, которая меняется вправо и влево на одинаковое число.

Найдём нули функции:

Суть в том, что мы отмечаем три точки на координатной плоскости и проводим ветви параболы, осознавая как именно растёт функции, функции x^2, то есть не надо ветви проводить как будто это уравнение прямой.

И чтоб всё было отмечено, найдём точки пересечения функции с осью Оу: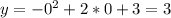 то есть (0;3)

1) При x∈(-∞;-1)∪(3;+∞) функция принимает отрицательные значения

При x∈(-1;3) функция принимает положительные значения

2) При x∈(-∞;1) функция растёт

При x∈(1;+∞) функция убывает

3) Минимальное значение -∞, достигается в точках (-∞;-∞) или (+∞;-∞)

Максимальное значение 4, достигается в точке (1;4)

Выражение: 3/4=(x+2)/8

ответ: 0.5-x/8=0

Решаем по действиям:
1) 3/4=0.75
  3.0|4_ _
  2_8_|0.75
   20
   2_0_
    0
2) (x+2)/8=x/8+2/8
3) 2/8=0.25
  2.0|8_ _
  1_6_|0.25
   40
   4_0_
    0
4) 0.75-(x/8+0.25)=0.75-x/8-0.25
5) 0.75-0.25=0.5
  -0.75
   _0_._2_5_
   0.50

Решаем по шагам:
1) 0.75-(x+2)/8=0
  1.1) 3/4=0.75
      3.0|4_ _
      2_8_|0.75
       20
       2_0_
        0
2) 0.75-(x/8+2/8)=0
  2.1) (x+2)/8=x/8+2/8
3) 0.75-(x/8+0.25)=0
  3.1) 2/8=0.25
      2.0|8_ _
      1_6_|0.25
       40
       4_0_
        0
4) 0.75-x/8-0.25=0
  4.1) 0.75-(x/8+0.25)=0.75-x/8-0.25
5) 0.5-x/8=0
  5.1) 0.75-0.25=0.5
      -0.75
       _0_._2_5_
       0.50

Решаем уравнение 0.5-x/8=0:

Решаем относительно x:
x=(-(-0.5))*8=0.5*8=4.