До момента начала движения мотоциклиста автомобиль проехал x*t км, по формуле: V=S/t, где V - скорость, S - путь, t - время, следовательно S=V*t, по условию задачи это x*t мотоциклисту потребовалось времени до встречи t мот= d/y, где по условию задачи d - путь мотоциклиста до встречи, а у - скорость смотри формулу V=S/t => t+S/V Общее расстояние между пунктами M и N складывается из трех частей: путь автомобиля до момента движения мотоциклиста, он нам известен x*t путь мотоциклиста до встречи, по условию это d путь автомобиля от момента движения мотоциклиста до встречи с ним, он нам не известен, но может быть вычислен по формуле s=V*T, где V это скорость автомобиля, по условию - x T - это время движения автомобиля до встречи, оно равно времени движения мотоциклиста. Мы его вычислили t мот=d/y, т.о. неизвестный отрезок пути равен s=x*d/y общее расстояние между пунктами равно S(MN)=x*t+x*d/y+d
x*t км,
по формуле: V=S/t, где V - скорость, S - путь, t - время,
следовательно S=V*t, по условию задачи это x*t
мотоциклисту потребовалось времени до встречи t мот= d/y,
где по условию задачи d - путь мотоциклиста до встречи, а у - скорость
смотри формулу V=S/t => t+S/V
Общее расстояние между пунктами M и N складывается из трех частей:
путь автомобиля до момента движения мотоциклиста, он нам известен x*t
путь мотоциклиста до встречи, по условию это d
путь автомобиля от момента движения мотоциклиста до встречи с ним, он нам не известен, но может быть вычислен по формуле s=V*T,
где V это скорость автомобиля, по условию - x
T - это время движения автомобиля до встречи, оно равно времени движения мотоциклиста. Мы его вычислили t мот=d/y,
т.о. неизвестный отрезок пути равен s=x*d/y
общее расстояние между пунктами равно
S(MN)=x*t+x*d/y+d
Для решения запишем формулу бинома Ньютона:
Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение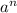
.
Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение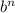
.
Рассмотрим многочлен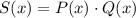
, где:
Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.
Для многочлена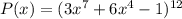
:
- степень определяется выражением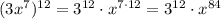
, то есть степень равна 84
- свободный член равен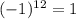
Для многочлена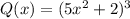
:
- степень определяется выражением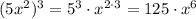
, то есть степень равна 6
- свободный член равен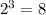
Наконец, для многочлена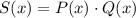
получим:
- степень определяется выражением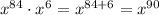
, то есть степень равна 90
- свободный член равен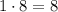
Сумма степени и свободного члена многочлена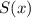
:
ответ: 98