Т.к. sin(x) - непрерывная функция, она интегрируема, и можно выбирать любое разбиение с любыми точками на нем. Разобьем [a,b] на n равных частей и возьмем значения функции в левых точках получившихся отрезков: ∑ sin(a + k*(b-a)/n) * (b-a)/n, где k = 0 .. n-1
Здесь были применены формулы cos(x+y) = cos(x)cos(y) - sin(x)sin(y) cos(x-y) = cos(x)cos(y) + sin(x)sin(y) Тогда sin(x)sin(y) = 1/2 (cos(x-y) - cos(x+y)) Где x = a + k*(b-a)/n, y = (b-a)/2n
y было выбрано так, чтобы все косинусы, кроме крайних, попадали в сумму с разными знаками и сокращались.
Исходная сумма ∑ sin(a + k*(b-a)/n) * (b-a)/n преобразуется к виду (b-a)/n * 1/(2sin( (b-a)/2n )) * ∑ [cos(a + (k-1/2)*(b-a)/n) - cos(a + (k+1/2)*(b-a)/n)], k = 0 .. n-1
Т.к. cos(a + (k + 1/2) * (b-a)/n) = cos(a + ((k+1)-1/2) * (b-a)/n), соответствующие слагаемые в сумме сокращаются, как и рассчитывалось. Т.е.
При n ⇒ ∞, это выражение стремится к cos(a) - cos(b)
Что касается коэффициента (b-a)/n * 1/(2sin( (b-a)/2n )) перед суммой, при n ⇒ ∞ синус стремится к своему аргументу, т.е. (b-a)/n * 1/(2sin( (b-a)/2n )) ⇒ (b-a)/n * 1/(2 * (b-a)/2n)) = 1
Т.е. сумма стремится cos(a) - cos(b) при n ⇒ ∞, причем этот предел по определению и является искомым определенным интегралом (диаметр разбиения (b-a)/n стремится к 0)
Примем за 1 - объем цистерны
Пусть t цис./ч - производительность "медленного" насоса.
Тогда 3t цис./ч - производительность "быстрого" насоса.
(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.
(t+3t)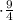
- объем работы системы из двух насосов за 2ч 15мин.
Получим уравнение: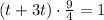
9t = 1
Значит,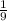
- цис./ч - производительность "медленного" насоса.
Тогда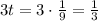
- цис./ч - производительность "быстрого" насоса.
Следовательно,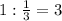
ч - потребуется "быстрому" насосу на заполнение цистерны.
ответ: 3 ч.
∑ sin(a + k*(b-a)/n) * (b-a)/n, где k = 0 .. n-1
Далее преобразуем слагаемые в разности косинусов:
sin(a + k*(b-a)/n) = sin(a + k*(b-a)/n) * sin( (b-a)/2n ) / sin( (b-a)/2n ) = 1/(2sin((b-a)/2n)) * [cos(a + (k-1/2)*(b-a)/n) - cos(a + (k+1/2)*(b-a)/n)]
Здесь были применены формулы
cos(x+y) = cos(x)cos(y) - sin(x)sin(y)
cos(x-y) = cos(x)cos(y) + sin(x)sin(y)
Тогда sin(x)sin(y) = 1/2 (cos(x-y) - cos(x+y))
Где x = a + k*(b-a)/n, y = (b-a)/2n
y было выбрано так, чтобы все косинусы, кроме крайних, попадали в сумму с разными знаками и сокращались.
Исходная сумма ∑ sin(a + k*(b-a)/n) * (b-a)/n преобразуется к виду
(b-a)/n * 1/(2sin( (b-a)/2n )) * ∑ [cos(a + (k-1/2)*(b-a)/n) - cos(a + (k+1/2)*(b-a)/n)], k = 0 .. n-1
Т.к. cos(a + (k + 1/2) * (b-a)/n) = cos(a + ((k+1)-1/2) * (b-a)/n), соответствующие слагаемые в сумме сокращаются, как и рассчитывалось. Т.е.
∑ [cos(a + (k-1/2)*(b-a)/n) - cos(a + (k+1/2)*(b-a)/n)] = cos(a - 1/2 (b-a)/n) - cos(a + (n - 1/2)*(b-a)/n)
При n ⇒ ∞, это выражение стремится к cos(a) - cos(b)
Что касается коэффициента (b-a)/n * 1/(2sin( (b-a)/2n )) перед суммой, при n ⇒ ∞ синус стремится к своему аргументу, т.е. (b-a)/n * 1/(2sin( (b-a)/2n )) ⇒ (b-a)/n * 1/(2 * (b-a)/2n)) = 1
Т.е. сумма стремится cos(a) - cos(b) при n ⇒ ∞, причем этот предел по определению и является искомым определенным интегралом (диаметр разбиения (b-a)/n стремится к 0)