Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
А
Английский язык
Х
Химия
Э
Экономика
П
Право
И
Информатика
У
Українська мова
Қ
Қазақ тiлi
О
ОБЖ
Н
Немецкий язык
Б
Беларуская мова
У
Українська література
М
Музыка
П
Психология
А
Алгебра
Л
Литература
Б
Биология
М
МХК
О
Окружающий мир
О
Обществознание
И
История
Г
Геометрия
Ф
Французский язык
Ф
Физика
Д
Другие предметы
Р
Русский язык
Г
География
Показать больше
Показать меньше
ElementalOfChaos
12.03.2020 02:38 •
Алгебра
Запишите выражение для нахождения суммы первых n членов прогрессии (bn) если : а)b1=1,q=5; б)b1=1,q=1/3 ' решить '
Показать ответ
Ответ:
вера571
11.06.2020 23:27
Сумма первых n членов геометрической прогрессии:
a)
б)
0,0
(0 оценок)
Популярные вопросы: Алгебра
anonymous18
24.02.2021 05:04
Алгебра, відніміть дроби...
стрелыамура2
02.05.2020 03:40
нужно продолжить решения...
валентина268
07.01.2023 23:23
Отрицательная дробь в чётной или нечётной степени....
Dimas2710
15.03.2022 04:03
1. Найти критические точки функции y = -12x - 3x² + 2x³. 2. Найти промежутки монотонности функции y = x³ – 3x² – 9x + 3. 3. Найдите точки экстремума функции y =...
teymurvalikhan1
18.10.2022 19:13
Sin 8a cos 2a - cos 8a sin 2a cos 2a cos 4a - sin 2a sin 4a...
melashich2004
01.08.2022 20:40
Варіант 2 №№1-4 по 0, №№5-8 - по №№9-11 - по 3°. Виконайте множення: 1) ap – ax +6a); 2) – t( a + b – 3). 4°. Винесіть за дужки спільний множник: 1) 9a – 9b=-9a-9b=9(a-b);...
sasha23z
16.12.2021 08:04
Для каких х значения функций у=0,5х+2 и y=3- 3х одновременно 1) положительны; 2) отрицательны; 3) больше 3; 4) меньше 3...
jeni1955ma
21.01.2020 00:09
Сума двох натуральних чисел доривнюе 15, а ризниця чисел обернених до них 1/18(дроб), знайдить ци числа...
Валерия3365
13.02.2020 09:59
Используя определение предела функции в точке, докажите, что...
maksimkakravchenko
20.02.2022 21:24
570. Пре дставьте в стандартном виде многочлен:а) - 8р* + 12p3 + 4р - 8р? + Зр?;б) 2aa2+a2 - 3a2+a3 -а;в) 3xx4 + 3xx3 - 5х2х3 – 5х2х;г) За: 462 — 0,8b. 4b2 - 2ab...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Сумма первых n членов геометрической прогрессии: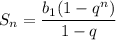
a)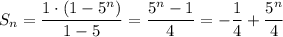
б)