Объяснение:
-первоначальная дробь.
-обратная ей дробь
+ = / *70x(x+3)
70x²+70(x+3)²=149x(x+3)
70x²+70*(x²+6x+9)=149x²+447x
70x²+70x²+420x+630=149x²+447x
140x²+420x-149x²-447x=-630
-9x²-27x+630=0/÷(-9)
x²+3x-70=0
D=9-4*1*(-70)=9+280=289=17²
x1==7
x2= =-10
первоначальная дробь или
Нехай чисельника початкового дробу буде -х ,тоді знаменник дорінює (х+3) , при цьому початковий дріб має вигляд х/(х+3), а обернутий (х+3)/х
Складемо рівняння:
х/(х+3)+(х+3)/х=149/70
70*(х²+х²+6х+9)-149(х²+3х)=0
140х²-149х²+420х-447х+630=0
-9х²-27х +630=0 скоротимо на 9 і помножимо на -1 отримаємо
х²+ 3х - 70=0
D=b²-4ac= 3²- 4*1*(-70)= 289=17
x= -10 (негативне) x=7
Таким чином, чисельник початкового дробу дорівнює 7, так як знаменик на 3 більший отримуємо дріб 7/10
Объяснение:
70x²+70(x+3)²=149x(x+3)
70x²+70*(x²+6x+9)=149x²+447x
70x²+70x²+420x+630=149x²+447x
140x²+420x-149x²-447x=-630
-9x²-27x+630=0/÷(-9)
x²+3x-70=0
D=9-4*1*(-70)=9+280=289=17²
x1=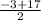 =7
=7
x2=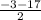 =-10
=-10
первоначальная дробь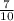 или
или 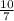
Объяснение:
Нехай чисельника початкового дробу буде -х ,тоді знаменник дорінює (х+3) , при цьому початковий дріб має вигляд х/(х+3), а обернутий (х+3)/х
Складемо рівняння:
х/(х+3)+(х+3)/х=149/70
70*(х²+х²+6х+9)-149(х²+3х)=0
140х²-149х²+420х-447х+630=0
-9х²-27х +630=0 скоротимо на 9 і помножимо на -1 отримаємо
х²+ 3х - 70=0
D=b²-4ac= 3²- 4*1*(-70)= 289=17
x= -10 (негативне) x=7
Таким чином, чисельник початкового дробу дорівнює 7, так як знаменик на 3 більший отримуємо дріб 7/10