Алгебра: Знайдіть координати вершини параболи : у=6+4х-2х²

Знайдіть координати вершини параболи : у=6+4х-2х²

Показать ответ

Ответ:

xeniapopsoip00ty7

02.10.2021 14:10

Катер проходит за 30 минут против течения реки такое же расстояние, какое проходит за 20 минут по течению реки. Найдите скорость катера в стоячей воде, если скорость течения реки равна 3 км/ч.

- - -

Скорость катера в стоячей воде обозначаем через u км/ч ;

v _ скорость течения реки (известно v = 3км/ч)

скорость катера против течения реки будет : (u -v) км/ч

скорость катера по течению реки будет : (u +v) км/ч

Можем написать уравнение :

t₁ *(u -v) = t₂*(u+v) ;

(30/60)*(u -3) = (20/60)*(u+3) ;

3*(u -3) = 2*(u+3) ;

3u -9 = 2u+6 ;

3u -2u= 6+9 ;

u =15 (км/ч)

ответ: 15 км/ч .

0,0(0 оценок)

Ответ:

Топтоппатимейкер

05.04.2023 04:39

a < 0

Объяснение:

Когда мы видим уравнения с x и y в квадрате и с одинаковыми коэффициентами перед ними, это наводит на мысль, что перед нами уравнение окружности. Оно имеет вид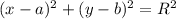 (x-a)^2+(y-b)^2=R^2 . Попробуем преобразовать его к данному виду. Для этого нужно поделить обе части на 2, чтобы коэффициент при старших членах был 1, и выделить полные квадраты:

$x^2-2x+y^2+4y+5-\dfrac{a}{2}=0\\x^2-2x+1-1+y^2+4y+4-4+5-\dfrac{a}{2}=0\\(x-1)^2-1+(y+2)^2-4+5-\dfrac{a}{2}=0\\(x-1)^2+(y+2)^2=\dfrac{a}{2}$

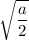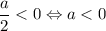Это окружность с радиусом $\sqrt{\dfrac{a}{2}}$ . Если радиус равен нулю, то окружность превращается в точку. Значит, окружности не существует, если не выполняется ОДЗ корня: $\dfrac{a}{2}$ .

Можно было рассуждать немного иначе: провести те же самые преобразования, но рассуждать не в терминах окружности, а в терминах суммы. В левой части сумма двух квадратов, каждый из них не меньше нуля. Значит, вся левая часть не меньше нуля, причём слагаемые друг от друга не зависят, поэтому в левой части можно представить любое неотрицательное число. Но тогда и правая часть не меньше нуля. Если же правая часть меньше нуля, то пара (x; y) не найдётся.

0,0(0 оценок)

Популярные вопросы: Алгебра