Знайдіть найбільше значення функції У=-х^2-6х+5 на проміжку (-4;-2)

1) F '(x)=1/3 - (4x^(-1)) ' = 1/3 + 4x^(-2)=1/3 + 4/x^2. (По-видимому, в условии описка:

f(x) должна равняться 1/3 + 4/x^2).  Так как х в знаменателе, х не=0, т.е. на интервале (-беск; 0) F(x) является первообразной для f(x)

2) a) не понятно;  б) F(x)=(3sin2x)/2 + C. По условию х=pi/4;  y=0 - это F(x). Тогда

(3sin(pi/2))+C=0,  3+C=0,  C=-3. Отсюда  F(x)=(3sin2x)/2 - 3

3)  a)  S=интеграл от 1 до 3 (x^3)dx = (x^4)/4 от 1 до 3 = 81/4  - 1/4 =80/4=20

б) найдем пределы интегрирования x^2-3x+4=4-x, x^2-2x=0,  x=0; 2

Прямая будет выше параболы на этом отрезке, поэтому

S= интеграл от 0 до 2 (4-x-x^2 +3x-4)dx= интеграл от 0 до 2 (-x^2+2x)dx=

=(-x^3/3  +x^2) от 0 до2 = -8/3  +4 = 1 целая 1/3 

Для исследования функции сначала нужно взять производную. Чтобы проще было взять воспользуемся формулой сложения степеней: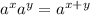 

Получим что: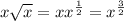  

Теперь перепишем функцию:

И берем производную:

Дальше найдем точку где производная обращается в 0.

Для этого решаем уравнение: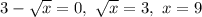  

Это будет точка экстремума. Но точка экстремума может быть как минимумом так и максимумом. Надо показать что это максимум. Как это делается. Есть 2 метода.
1 метод:

Рассмотрим как ведет себя производная при x<9 и при x>9.  Очевидно, что при x>9 производная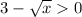  . Значит функция растет. При x>9, наоборот  . Для любых положительных х, вторая производная будет меньше нуля, т.е y''<0. Это необходимое и достаточное условие, чтобы функция была выпуклой вверх. Т.к. функция выпулкая вверх, то точка экстремума будет точкой максимума. ч.т.д

ответ: точка максимума x=9, значение функции в этой точке y(9)=10