Первоначальная стоимость группы объектов на 1 января составляла 425 тыс. руб., срок фактической эксплуатации – 2 года.
Рассчитайте остаточную стоимость и коэффициент износа на ту же дату, если амортизация начисляется а) линейным б уменьшаемого остатка (коэффициент ускорения 2); в суммы чисел лет срока полезного использования. Для данной группы объектов определен срок полезного использования 10 лет.
При решении данной задачи исходим из того, что остаточная стоимость представляет собой первоначальную стоимость за минусом износа, а сумма начисленного износа – сумму амортизации за весь период фактического использования объекта. Поэтому решение начнем с расчета суммы износа по каждому из амортизации.
а) Произведем расчет по линейному Годовую сумму амортизации определяем по формуле
Норма амортизации может быть установлена следующим образом:
На = 1 / Т · 100
Рассчитаем норму амортизации при сроке полезного использования 10 лет:
На = 1 / 10 · 100 = 10 %.
Амортизация за год составит
А = 160 · 10 / 100 = 16 тыс. руб.
При этом сумма амортизации каждый год одинакова, поэтому износ за три года равен
И = 16 · 3 = 48 тыс. руб.
б) Проведем расчет по уменьшаемого остатка. Для определения амортизации используем следующую формулу:
Амортизация за первый год составит
А1 = 160 · 2 · 10 / 100 = 32 тыс. руб.,
за второй год –
А2 = (160 – 32) · 2 · 10 / 100 = 25,6 тыс. руб.,
за третий год –
А3 = (160 – 32 – 25,6) · 2 · 10 / 100 = 20,48 тыс. руб.
Износ за три года рассчитаем как сумму амортизации за три года:
И = 32 + 25,6 + 20,48 = 78,08 тыс. руб.
в) Произведем расчет по суммы лет. Для определения годовой амортизации используем следующую формулу:
А3 = 160 · 8 / (10 (10 + 1) / 2) = 23,27 тыс. руб.
Сложив суммы амортизации за три года получим сумму износа:
И = 29,09 + 26,18 + 23,27 = 78,54 тыс. руб.
Зная суммы износа, рассчитанные различными можно вычислить остаточную стоимость и коэффициент износа, используя формулу
Коэффициент износа найдем по формуле
Подставив значения, получим:
а) линейный
Сост = 160 – 48 = 112 тыс. руб.,
Кизн = 48 / 160 · 100 = 30 %;
б уменьшаемого остатка:
Сост = 160 – 78,08 = 81,92 тыс. руб.,
Кизн = 78,08 / 160 · 100 = 48,08 %;
в суммы лет:
Сост = 160 – 78,54 = 81,46 тыс. руб.,
Кизн = 78,54/160 · 100 = 49,1 %.
Таким образом, по результатам решения данной задачи видно, что нелинейные методы позволяют списать большую часть стоимости в первые годы эксплуатации объекта основных средств.
На развитие аккаунта в TikTok Федя взял в кредитной организации кредит. По истечении первого года он вернул в банк в счет погашения обязательств 1/3 от всей суммы кредита, которую он должен был банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму на 16% превышающую величину полученного кредита. Под какой процент Федя брал кредит?
Объяснение:
Пусть сумма кредита S , проценты кредита к %. Тогда
сумма долга через 1 год : S+S* = S(1+0,01k) ;сумма долга через 2 года , с учетом ,что 1/3 от всей суммы погашена( фактически осталось 2/3) : == .
Т.к после 2 года он внес в банк сумму на 16% превышающую величину полученного кредита , т.е. S+0,16S=1,16S , то составим уравнение =1,16S |:S*(3/2)
Первоначальная стоимость группы объектов на 1 января составляла 425 тыс. руб., срок фактической эксплуатации – 2 года.
Рассчитайте остаточную стоимость и коэффициент износа на ту же дату, если амортизация начисляется а) линейным б уменьшаемого остатка (коэффициент ускорения 2); в суммы чисел лет срока полезного использования. Для данной группы объектов определен срок полезного использования 10 лет.
При решении данной задачи исходим из того, что остаточная стоимость представляет собой первоначальную стоимость за минусом износа, а сумма начисленного износа – сумму амортизации за весь период фактического использования объекта. Поэтому решение начнем с расчета суммы износа по каждому из амортизации.
а) Произведем расчет по линейному Годовую сумму амортизации определяем по формуле
Норма амортизации может быть установлена следующим образом:
На = 1 / Т · 100
Рассчитаем норму амортизации при сроке полезного использования 10 лет:
На = 1 / 10 · 100 = 10 %.
Амортизация за год составит
А = 160 · 10 / 100 = 16 тыс. руб.
При этом сумма амортизации каждый год одинакова, поэтому износ за три года равен
И = 16 · 3 = 48 тыс. руб.
б) Проведем расчет по уменьшаемого остатка. Для определения амортизации используем следующую формулу:
Амортизация за первый год составит
А1 = 160 · 2 · 10 / 100 = 32 тыс. руб.,
за второй год –
А2 = (160 – 32) · 2 · 10 / 100 = 25,6 тыс. руб.,
за третий год –
А3 = (160 – 32 – 25,6) · 2 · 10 / 100 = 20,48 тыс. руб.
Износ за три года рассчитаем как сумму амортизации за три года:
И = 32 + 25,6 + 20,48 = 78,08 тыс. руб.
в) Произведем расчет по суммы лет. Для определения годовой амортизации используем следующую формулу:
Амортизация за первый год составит
А1 = 160 · 10 / (10 (10 + 1) / 2) = 29,09 тыс. руб.,
за второй год –
А2 = 160 · 9 / (10 (10 + 1) / 2) = 26,18 тыс. руб.,
за третий год –
А3 = 160 · 8 / (10 (10 + 1) / 2) = 23,27 тыс. руб.
Сложив суммы амортизации за три года получим сумму износа:
И = 29,09 + 26,18 + 23,27 = 78,54 тыс. руб.
Зная суммы износа, рассчитанные различными можно вычислить остаточную стоимость и коэффициент износа, используя формулу
Коэффициент износа найдем по формуле
Подставив значения, получим:
а) линейный
Сост = 160 – 48 = 112 тыс. руб.,
Кизн = 48 / 160 · 100 = 30 %;
б уменьшаемого остатка:
Сост = 160 – 78,08 = 81,92 тыс. руб.,
Кизн = 78,08 / 160 · 100 = 48,08 %;
в суммы лет:
Сост = 160 – 78,54 = 81,46 тыс. руб.,
Кизн = 78,54/160 · 100 = 49,1 %.
Таким образом, по результатам решения данной задачи видно, что нелинейные методы позволяют списать большую часть стоимости в первые годы эксплуатации объекта основных средств.
На развитие аккаунта в TikTok Федя взял в кредитной организации кредит. По истечении первого года он вернул в банк в счет погашения обязательств 1/3 от всей суммы кредита, которую он должен был банку к этому времени, а еще через год в счет полного погашения кредита он внес в банк сумму на 16% превышающую величину полученного кредита. Под какой процент Федя брал кредит?
Объяснение:
Пусть сумма кредита S , проценты кредита к %. Тогда
сумма долга через 1 год : S+S*Т.к после 2 года он внес в банк сумму на 16% превышающую величину полученного кредита , т.е. S+0,16S=1,16S , то составим уравнение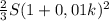
=1,16S |:S*(3/2)
(1+0,01к)²=1,74 , 1+0,01к=√1,74 , 0,01к=√1,74-1 , к=100(√1,74-1)
к≈31 . Кредит взят по 31% годовых.