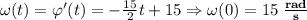1.36 Если в изображенной схеме (см.рис.) E1=2 В; R1=2,5 Ом, а параметры эквивалентного генератора относительно ветви R1, E1 составляют: EГ = 1 В; RГ = 1,5 Ом, то ток в этой ветви равен….
ответ: 1) I = 1/2 А 2) I= 3/4 А 3) I = 1/4 А 4) I = 1 А
A' - ? ΔU - ? Q - ? m = 6 г = 0,006 кг T = 303 К p = const V₂ = 2 V₁ R = 8,31 Дж/(моль*K ) M(O₂) = 16 * 10^(-3) кг/моль Решение:
1) для изобарного процесса (p = const) 1-ый закон термодинамики имеет вид: Q = ΔU + A', где A' = pΔV 2) из уравнения Менделеева-Клапейрона: pV₁ = (m/M)RT₁ 2pV₁ = (m/M)RT₂ разделив одно уравнение на другое, получим: Т₂ = 2T₁ (для вывода Т₂ = 2T₁ так же можно использовать закон Гей-Люссака) вычев из второго уравнения первое, получим: pΔV = (m/M)R(T₂ - T₁) = (m/M)RT₁ = A' 3) ΔU = (i/2)(m/M)RΔT, где i - число степеней свободы (i=3) ΔU = (3/2)(m/M)R(T₂ - T₁) = (3/2)(m/M)RT₁ 4) выполните расчеты самостоятельно: A' = (m/M)RT₁ = ... ΔU = (3/2)(m/M)RT₁ = ... Q = ΔU + A' = (3/2)(m/M)RT₁ + (m/M)RT₁ = (5/2)(m/M)RT₁
ΔU - ?
Q - ?
m = 6 г = 0,006 кг
T = 303
К p = const
V₂ = 2
V₁ R = 8,31 Дж/(моль*K
) M(O₂) = 16 * 10^(-3) кг/моль
Решение:
1) для изобарного процесса (p = const) 1-ый закон термодинамики имеет вид: Q = ΔU + A', где A' = pΔV 2) из уравнения Менделеева-Клапейрона: pV₁ = (m/M)RT₁ 2pV₁ = (m/M)RT₂ разделив одно уравнение на другое, получим: Т₂ = 2T₁ (для вывода Т₂ = 2T₁ так же можно использовать закон Гей-Люссака) вычев из второго уравнения первое, получим: pΔV = (m/M)R(T₂ - T₁) = (m/M)RT₁ = A' 3) ΔU = (i/2)(m/M)RΔT, где i - число степеней свободы (i=3) ΔU = (3/2)(m/M)R(T₂ - T₁) = (3/2)(m/M)RT₁ 4) выполните расчеты самостоятельно: A' = (m/M)RT₁ = ... ΔU = (3/2)(m/M)RT₁ = ... Q = ΔU + A' = (3/2)(m/M)RT₁ + (m/M)RT₁ = (5/2)(m/M)RT₁
2.3 Момент инерции системы точек вычисляется по формуле: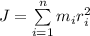 , где
, где 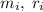 - соответственно масса i-той точки и расстояние от i-той точки до оси.
- соответственно масса i-той точки и расстояние от i-той точки до оси.
Для начального положения: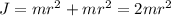 ; для конечного:
; для конечного: 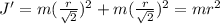 ; Получили, что момент инерции системы уменьшился в два раза.
; Получили, что момент инерции системы уменьшился в два раза.
2.2 Так как зависимость параболическая, то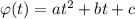 ;
;
Заметим, что коэффициент c - есть ордината точки пересечения параболы с осью OY (действительно, чтобы в этом убедиться достаточно подставить x=0).
Координаты вершины также достаточно просто вычислить. Имеем: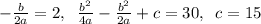 ; Отсюда легко вывести, что
; Отсюда легко вывести, что 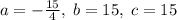 ; Итак,
; Итак, 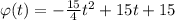 , значит,
, значит,