Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Шарик массой m1=34г, имеющий кинетическую энергию к=56дж налетает на покоящийся шар массой m2=164г. с какой скоростью будут двигаться шары после абсолютного столкновения? ответ в метрах в секунду, 3 знака после запятой. вот так я решал: к=(m1*v^2 )/2 v^2=(k*2)/m1 v=корень((k*2)/m1) v=корень((56*2)/34)=1.815 получили скорость шара n1 до столкновения. в результате абсолютно удара (слипания) частицы движутся с одинаковой скоростью . по закону сохранения импульса m1*v=(m1+m2)*u,по закону сохранения энергии (m1*v^2)/2=(m1+m2)*u^2/2/ отсюда я нашел: mv=(m1+m2)*u, 34*1.815=(34+164)*u 61.71 =198*u u=61.71/198 u=0.327 надо перевести в килограммы. ответ 9,86 м/с
11,25 м
Объяснение:
Если решать эту задачу по школьному, без привлечения инструментария матанализа, то рассуждать можно следующим образом, - в любой точке траектории ускорение свободного падения может быть разложено на две составляющих - вдоль касательной к траектории (нормальное ускорение) и вдоль нормали к траектории (центростремительное ускорение), нам нужна вторая величина, так как она позволяет рассчитать искомый радиус. В наивысшей точке подъема мяча, очевидно, что центростремительное ускорение целиком совпадает с ускорением свободного падения:
Откуда:
Горизонтальная составляющая скорости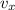 будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
будет везде одинакова и равна (учтем что 54 км/ч=15 м/с):
Искомый радиус кривизны траектории: