1) вывести формулу для момента инерции каркаса равнобедренного треугольника массой m, с длиной боковых сторон, равной l, и углом при вершине, равном α, относительно оси вращения, проходящей вдоль высоты треугольника.

Показать ответ

Ответ:

tatiana2017D

11.12.2021 09:07

Рассмотрим 2 варианта решения: один потривиальнее, а другой поизвращеннее, но и поинтереснее =)

1 вариант - не будем учитивать изменения g.

E_p=Mgh ; $h=\frac{E_p}{mg}$

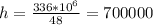Произведем подсчеты: $h=\frac{336*10^6}{48}=700000$ м

2 вариант - учтем изменение g.

Сила тяжести, действующая на предмет, находящийся на поверхности земли со стороны земли равна:

$F_T=G\frac{mM}{R^2}$

Поскольку тело покоится относительно земли, уравнение принимает вид:

$mg=G\frac{mM}{R^2}$

Сокращая на g, находим:

$g=G\frac{M}{R^2}$

Теперь поднимем тело относительно земли на высоту h:

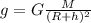
Δ $g=G\frac{M}{(R+h)^2}$

Аналогичным с первой задачей образом находим:

$h=\frac{E_p}{mg}=\frac{E_p}{mG\frac{M}{(R+h)^2}}=\frac{(E_p)(R+h)^2}{mMG}$

Считать мне оказалось внезапно лень, так что возьмите таблицы геофизических постоянных планеты Земля и посчитайте. Если Вы все сделали правильно, то ответ почти не должен отличаться от полученного нами в первом варианте.

0,0(0 оценок)

Ответ:

wehter83

01.08.2021 18:40

Поверь вычисления!!... точность не гарантирую...

Вес тела на полюсе P1

P1=m*g (вниз действует сила тяжести планеты, вверх - сила реакции опоры. По третьему закону Ньютона вторая сила численно равна весу тела, поскольку есть причиной возникновения силы реакции опоры)

Вес тела на экваторе P2

P2=m*(g-a)=m*(g-v^2/R) (На экваторе тело движется с цетростремительным ускорением, направленым к центру планеты. По второму закону Ньютона сила, вызывающая это ускорение равна силе теяжести минус сила реакции опоры. Дальше аналогично как в первом случае.

Для нахождения центростремительного ускорения нужно выразить скорость для движения тела по окружности.

v=2*п*R/T

подставить в формулу для веса

P2=m*(g-(4*п^2*R)/T^2) масса при делении в дальнейшем сократиться, проблема найти g этой планеты и её радиус R.

Вспоминаем закон всемирного тяготения и записываем силу тяжести, действующую на этой планете через две разные формулы. Вторая формула справедлива для тела, которое находится на поверхности планеты.

G*M*m/R^2=g*m

маленькая масса (масса тела) сокращается

G*p*V/R^2=g

Массу большую (планеты) расписываем как произведение плотности планеты на объём, где объём выражаем как объём шара

G*p*4*п*R^3/(3*R^2)=g

Выражаем отсюда радиус планеты.

R=3*g/(4*п*G*p)

Подставляем и выносим два общих множетеля: массу тела и ускорение свободного падения на этой планете:

P2=m*g*(1- 3*п/(T^2*G*p))

Находим отношение веса тела на полюсе и веса тела на экваторе:

P1/P2=m*g/[ m*g*( 1- 3*п/(T^2*G*p) ) ] =1/[1-3*п/( T^2*G*p)]

P1/P2=1/[1-3*3,14/(10^10*6,67*10^(-11)*700) ] =1,0205=102,05%