4. Определите минимальную скорость, при которой автомобиль успеет остановиться перед препятствием, если он начинает тормозить на расстоянии 25 м от препятствия, а коэффициент трения шин об асфальт равен 0,8.

Показать ответ

Ответ:

Патрисия2000

13.11.2020 06:27

Из курса физики известно, что наибольшая дальность полета достигается, когда скорость направлена под углом 45° к горизонту.

Дальность полета:

L = V₀²·sin (2α) / g

тогда:

V₀² =g·L / sin (2α) = 10·90 / 1 = 900 (м/с)²

V = 30 м/с или 108 км/ч

Время полета:

t = 2·V₀·sin 45° / g = 2·30·√2 / (2·10) ≈ 4,24 с

Если же скорость принять 202 км/ч ≈ 56 м/с

Тогда можно пнуть и под углом

sin (2α) = L·g / V₀² = 90·10/56² ≈ 0,827

2α = 56°

α = 28°

В этом случае время полета мяча

t = 2·V₀·sin 28° / g = 2·56·0,4695/10 ≈ 5, 26 с

Вывод: Можно пнуть мяч под углом 45°, в этом случае скорость мяча всего 108 км/ч

Если же скорость мяча рекордная (202 км/ч), то направление удара может быть и меньше 45⁰

0,0(0 оценок)

Ответ:

Assassin5510

21.01.2023 13:39

Задача на бросок под углом к горизонту. Уравнения движения камня:

$x = V_0tcos\alpha\\ y = V_0tsin\alpha - \frac{gt^{2}}{2}$

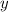По условию, траектория камня проходит через точку с координатами = 20 и = 15.

Имеем систему:

$\left \{ {{V_0tcos\alpha=20} \atop {V_0tsin\alpha-\frac{gt^2}{2}=15}} \right.$

Из первого уравнения выразим время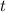 и подставим во второе уравнение:

$\left \{ {{t = \frac{20}{V_0cos\alpha}} \atop {\frac{20V_0sin\alpha}{V_0cos\alpha}}-\frac{20^2g}{2V_0^2cos^2\alpha} = 15} \right.$

Преобразуем второе уравнение:

$\left \{ {{t = \frac{20}{V_0cos\alpha}} \atop 20tg\alpha-\frac{200g}{V_0^2cos^2\alpha} = 15}$

Из второго уравнения несложно выразить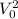 V_0^2 :

$V_0^2 = \frac{200g}{(20tg\alpha-15)cos^2\alpha} = \frac{200g}{20tg\alpha*cos^2\alpha-15cos^2\alpha}$ (&)

Для того, чтобы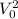 V_0^2 было наименьшим, необходимо, чтобы знаменатель дроби в правой части принимал как можно большее значение, так как величина числителя фиксирована.

Заметим, что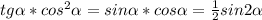 $tg\alpha *cos^2\alpha = sin\alpha *cos\alpha = \frac{1}{2} sin2\alpha$ , а также 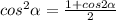$cos^2\alpha = \frac{1+cos2\alpha}{2}$ (формулы двойного угла).

Тогда

$20tg\alpha*cos^2\alpha-15cos^2\alpha = 10sin2\alpha - 15(\frac{1+cos2\alpha}{2} ) = 10sin2\alpha - 7,5cos2\alpha - 7,5 = \sqrt{10^2+7,5^2} sin(2\alpha +\phi) - 7,5$

(в последнем переходе воспользовались формулой вс аргумента).

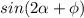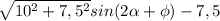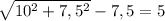Понятно, что максимальное значение $sin(2\alpha +\phi)$ это 1. Тогда максимальное значение выражения $\sqrt{10^2+7,5^2} sin(2\alpha +\phi) - 7,5$ есть $\sqrt{10^2+7,5^2} - 7,5 = 5$ .