Батарею из шести параллельно соединенных лейденских банок, каждая ёмкостью 4•10*10 ф, питается напряжением 80к/в одна из банок пробивается. определить изменение энергии батареи банок.
Введем систему координат так, чтобы плоскость P являлась плоскостью Oxy. Скорость частицы тогда представима в виде
т.е в виде суммы проекции на плоскость и на перпендикуляр плоскости. Сила, же, действующая на частицу, всегда перпендикулярна , но так как она перпендикулярна и скорости частицы, мы делаем вывод, что
Значит z-проекция скорости не меняется и частица смещается с постоянной скоростью вдоль перпендикуляра к плоскости. Также мы видим, что сила все время перпендикулярна компоненте скорости , значит она не меняет и ее величины (v cos α), а меняет только направление в плоскости. Отсюда глобальный вывод: модуль скорости частицы постоянен, значит постоянен и модуль силы, действующий на нее.
Без ограничения общности можно считать, что векторы , и образуют правую тройку. Тогда
Отметим что множитель F/(mv_0 cos α) постоянен в любом варианте задачи, обозначим его как ω. Продифференцируем первую строчку
Аналогично
Это все уравнения колебаний. Без ограничения общности можно считать, что начальная скорость частицы направлена вдоль оси Ox, тогда
Тогда после однократного интегрирования получим
Мы вольны выбирать какие хотим постоянные интегрирования, поскольку пока выбор положения начала координат в плоскости Oxy можно скорректировать. Удобнее всего вид, приведенный выше, в этом случае видно, что точка в плоскости движется по окружности с периодом
и радиусом
Значит траектория частицы в пространстве это спираль с радиусом R и шагом
В первом случае радиус и шаг спирали прямо пропорциональны начальной скорости, во втором - обратно пропорциональны
Введем систему координат так, чтобы плоскость P являлась плоскостью Oxy. Скорость частицы тогда представима в виде
т.е в виде суммы проекции на плоскость и на перпендикуляр плоскости. Сила, же, действующая на частицу, всегда перпендикулярна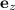 , но так как она перпендикулярна и скорости частицы, мы делаем вывод, что
, но так как она перпендикулярна и скорости частицы, мы делаем вывод, что
Значит z-проекция скорости не меняется и частица смещается с постоянной скоростью вдоль перпендикуляра к плоскости. Также мы видим, что сила все время перпендикулярна компоненте скорости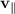 , значит она не меняет и ее величины (v cos α), а меняет только направление в плоскости. Отсюда глобальный вывод: модуль скорости частицы постоянен, значит постоянен и модуль силы, действующий на нее.
, значит она не меняет и ее величины (v cos α), а меняет только направление в плоскости. Отсюда глобальный вывод: модуль скорости частицы постоянен, значит постоянен и модуль силы, действующий на нее.
Без ограничения общности можно считать, что векторы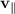 ,
, 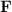 и
и 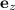 образуют правую тройку. Тогда
образуют правую тройку. Тогда
Отметим что множитель F/(mv_0 cos α) постоянен в любом варианте задачи, обозначим его как ω. Продифференцируем первую строчку
Аналогично
Это все уравнения колебаний. Без ограничения общности можно считать, что начальная скорость частицы направлена вдоль оси Ox, тогда
Тогда после однократного интегрирования получим
Мы вольны выбирать какие хотим постоянные интегрирования, поскольку пока выбор положения начала координат в плоскости Oxy можно скорректировать. Удобнее всего вид, приведенный выше, в этом случае видно, что точка в плоскости движется по окружности с периодом
и радиусом
Значит траектория частицы в пространстве это спираль с радиусом R и шагом
В первом случае радиус и шаг спирали прямо пропорциональны начальной скорости, во втором - обратно пропорциональны
Объяснение:
Дано:
x(t) = Xmax·cos (ω·t)
m = 5 г = 0,005 кг
ν = 0,5 Гц
Xmax = 3 см = 0,03 м
x = 1,5 см = 0,015 м
V - ?
F - ?
1)
Находим циклическую частоту:
ω = 2·π·υ = 2·π·0,5 = π с⁻¹
2)
Находим косинус фазы:
1,5 = 3·cos (π·t)
cos (π·t) = 1,5 / 3 = 0,5
Тогда:
sin (π·t) = √ (1 - 0,5²) ≈ 0,866
3)
Скорость - первая производная от координаты:
V = x' = - ω·Xmax·sin (ω·t) = - π·0,015·0,866 ≈ - 0,013·π ≈ - 0,04 м/с
или V = - 4 см/c
4)
Ускорение - первая производная от скорости:
a = V' = -ω²·Xmax·cos (ω·t)
a = - π²·0,03·0,5 = - 0,015·π² ≈ - 0,15 м/с²
Тогда модуль силы:
F = m·|a| = 0,005·0,15 = 0,75 мН