Решение: При равноускоренном движении тела пройдённый путь S определяется формулой: S = V0 * t + a * t2 / 2, где V0 - начальная скорость тела, t - время движения, a - ускорение при движении. Так как мотоциклист начинает своё движение из состояния покоя V0 = 0 м/с, то формула примет вид: S = a * t2 / 2.
t = √(2 * S / а).
t = √(2 * 1000 м / 0,8 м/с2) = 50 с.
Конечную скорость мотоциклиста V выразим из формулы для ускорения: a = (V - V0) / t.
У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.
V0 = 0 м/с.
S = 1 км = 1000 м.
a = 0,8 м/с2.
Найти:
t - ?
V - ?
Решение:
При равноускоренном движении тела пройдённый путь S определяется формулой: S = V0 * t + a * t2 / 2, где V0 - начальная скорость тела, t - время движения, a - ускорение при движении. Так как мотоциклист начинает своё движение из состояния покоя V0 = 0 м/с, то формула примет вид: S = a * t2 / 2.
t = √(2 * S / а).
t = √(2 * 1000 м / 0,8 м/с2) = 50 с.
Конечную скорость мотоциклиста V выразим из формулы для ускорения: a = (V - V0) / t.
V = V0 + a * t.
V = a * t.
V = 0,8 м/с2 * 50 с = 40 м/с.
ответ: t = 50 с, V = 40 м/с.
300м
Объяснение:
Граф. метод։
У нас на графике трапеция. Перемещение в данном случае равна площади под графиком(Если б скорость уходила бы в минус, тогда для рассчётов вектора перемещения нам понадобилось бы вычесть площадь минусовой части V). Площадь трапеции равна полусумме его оснований умноженное на её высоту.
⇒|S(вектор перемещения)| =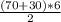
= 300м
Анал. метод։
0) V₀ = 0м/c, V₁ = 6м/c, Δt = 30с
⇒ a₀ = (V₁-V₀)/Δt = 0.2м/c²
⇒ S₀ = a₀Δt²/2 = 90м
1) a₁ = 0м/c²
⇒ S₁ = V₁ × t₁ = 6 × 30 = 180м
2) V₁ = 6м/c V₂ = 0 Δt = 10с
⇒ a₂ = -0.6м/c²
⇒ S₂ = V₁×Δt + a₂Δt²/2 = V₁²/(2×a₂) = 30м
⇒ ∑S = 90 + 180 + 30 = 300м