Для автогонок разрабатывают заправочные станции, которые в разы мощнее обычных бензоколонок. это связано с тем что требуется как можно быстрее заправить автомобиль во время остановки. представим, я что топливо подается в бензобак автомобиля со скоростью q=12 л/с. с какой средней скоростью выливается топливо из конца заправочного шланга, если площадь его сечения составляет s=15 см^2? ответ выразить в м/с, округлив до целых.
224.5 кДж
Объяснение:
Два замечания:
Параметры, которые у использовались в решении: теплоемкость чугунаДано: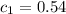
кДж / (кг °C), m₁ = 500 г = 0,5 кг, 
кДж / (кг °C),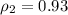 
кг/л, V₂ = 0,5 л, t₁ = 20°, t₂ = 230°
Найти: количество теплоты Q
Теплота, которая необходима для нагрева чугуна:
Q₁ = c₁ m₁ (t₂ - t₁) = 56.7 кДж
Масса масла:
m₂ = ρ₂ V₂ = 0.47 кг
Теплота, которая необходима для нагрева масла:
Q₂ = c₂ m₂ (t₂ - t₁) = 167,8 кДж
Общее количество теплоты:
Q = Q₁ + Q₂ = 224.5 кДж
ответ: 2,2 * 10^5 Дж
Объяснение:
Для начала проясним некоторые неточности подсолнечное масло до температуры 320 °С нагреть не получится ( это чисто физически невозможно так как температура кипения подсолнечного масла 230 °С ) так что буду считать то что это опечатка
Дано :
m1 ( масса чугуна ) = 500 г = 0,5 кг
V2 ( объём масла ) = 0,5 л = 0,5 * 10^-3 м³
tн ( начальная температура обоих тел ) = 20 °С
tк ( конечная температура обоих тел ) = 230 °С
с1 ( теплоёмкость чугуна ) = 500 Дж/кг*°С
c2 ( теплоёмкость подсолнечного масла ) = 1700 Дж/кг*°С
р2 ( плотность подсолнечного масла ) = 925 кг/м³
Q - ?
Q = Q1 + Q2
Q = c1m1( tк - tн ) + c2m2( tк - tн )
Q = c1m1( tк - tн ) + c2р2V2( tк - tн )
Q = 500 * 0,5 ( 230 - 20 ) + 1700 * 925 * 0,5 * 10^-3 ( 230 - 20 ) ≈ 2,2 * 10^5 Дж